最流行和使用最活跃

具有自适应学习速率（由RMSProp和AdaDelta代表）的算法族都表现得相当鲁棒，不分伯仲，没有哪个算法能脱颖而出，拨得头筹。

在本书第三部分讨论的一个常用策略是使用相同的输入数据集，用非监督模型训练出来的参数来初始化监督模型

自适应学习率算法

可惜

多了个”权“

最终的观点还是建议在传统优化算法上研究怎样选择更佳的初始化点，来实现目标更切实可行。

却和所有解决方案南辕北辙，

用舍近求远的方法来求解问题。

要抛掷n次硬币都正面朝上的难度是指数级的

生成的

DAE的机制是允许学习容量很高的编码器

相似

多个

此任务不仅和其他任务一样从降维技术中获取简单受益，更进一步地在某些低维空间中带来高效搜索性能。

a stack of RBMs

“栈式” RBM

驱动力

相比普通任务，信息检索从降维技术中获得的受益更多

Like many other machine learning algorithms,autoencoders exploit the idea that data concentrates around a low-dimensional manifold or a small set of such manifolds, 如同其它的机器学习算法,自编码器也探索了集中在低维流形上的数据或者此类流形的小数据集上的想法

他们的方法除了最小化重构误差这一监督目标项之外，还在隐藏层加入了噪音，目地是通过引入重构误差和注入噪音来改善泛化能力

探索了一些同样的方法和目标

无意义

在RBM上应用得分匹配后

去噪得分匹配算法

隐变量

本质上

深度特性也能帮助在训练一些函数时使所需要的数据量呈指数级降低。

指数级的降低

SGD及相关的minibatch亦或更广义的基于梯度优化的在线学习算法，一个重要的性质是每一步更新的计算时间不依赖训练样本数目的多寡。

但又不能太大导致严重的震荡

选择一个比在效果上表现最佳的学习率更大的学习率。

最优初始学习率的效果会好于大约迭代100次左右后最佳的学习率

那么学习过程会很缓慢

如果学习率太小

这更像

应该谨慎的参考这个问题的大部分指导

学习率

也主张，应该可以通过分析来表明连续时间的梯度下降会逃离而不是吸引到鞍点，不过， 对梯度下降在更多的使用场景来说，情况或许会有不同。

但是 在实际情况中 我们通过设置更多参数，很容易发现针对大型网络来说还不错的解决方案。

说明： 目前的翻译 有三个定语，太冗长。

则负对数似然可以无限趋近但不会等于零。

按照数据生成分布抽取m个小批量（独立同分布的）样本，通过计算它们梯度均值，

应用最广的

在现实中研究优化算法的性能上界仍然是学术界的重要目标

想要对优化算法是否能完成此目标进行理论分析是非常困难的

输出光滑的连续值

困难

局部下降不确定能不能找到有效解的短路径

无限制

若J(θ)J(θ)J(\Vtheta)是当前点θθ\Vtheta的病态条件

先决条件

无穷

而是当随着训练模型逐渐稳定后，收敛于某个值。

不一定存在

找到

代理

噪音

在更详细地描述循环网络之后

系数？

时刻

一定

各时刻

各时刻

膨胀的

explosion 建议翻译成 “膨胀”

当计算图变的极深时，神经网络优化算法会面临的另外一个难题就是长期依赖问题——由于变深的结构使模型丧失了学习到先前信息的能力，让优化变得极其困难。 深层的计算图不仅前馈网络中存在，在循环神经网络（在第十章中描述）结构中也是一样的，因为要在很长时间序列的各时刻重复操作相同的网络模块，并且模型参数共享，这使问题更加凸显。

说明：

这段感觉原文表述就有些问题，读起来感觉意思不连贯，在此小节并没有详说“长期依赖”是个什么东西，我调整了一下， 增加已经对长期依赖的简单说明来呼应标题，在破折号后面的一句行文解释来说明长期依赖对优化的困难，后接作者描述就显得意思上连贯了。

隐变量

可能会使大量已完成的优化工作成为无用功。

目前情况还不清楚。

鞍点扩散对于训练算法来说有哪些影响呢？

较优的可行解

简化

代理损失函数

以便用于像分类这样的任务

联结

其

深度自编码器至少要包含一层额外的隐藏层，在隐藏单元足够多的情况下能以任意精度近似任何从输入到编码的映射。

深度结构

各自

使得

过大

差异

差异

我们也可以通过改变重构误差项来得到一个能学到有用信息的自编码器

趋向

它虽不是一个先验

它

两句合并 “不像其它正则项如权重衰减——没有直观的贝叶斯解释。”

一般用来

不必

这样的能力

超完备

赋予的容量过大

我们已经知道

解码

类似的

再循环算法更具生物学意义，不过较少引入到机器学习领域。

不同于

概念推而广之

将输入数据按照不同方面划定主次顺序

限制

加一些约束，让它只能近似的复制

不应该将自编码器设计成输入到输出完全相等

non-trivial depth 我想直译较为生硬，不是太好理解 此句调整为 “这是有一定深度的网络其最主要的优点”

历史展望

第一项损失函数缺少一个右括号

缺少一个右括号

缺少一个右括号

不太通顺

his means that an autoencoder with a single hidden layer is able to represent the identity function along the domain of the data arbitrarily well.

这意味着具有单隐层的自编码器在数据域内能逼近任意恒等函数。

we can think of the entire sparse autoencoder framework as approximating maximum likelihood training of a generative model that has latent variables.

这句话是否可以帮助理解

Their encodings are naturally useful because the models were trained to approximately maximize the probability of the training data rather than to copy the input to the output.呢？ 近似最大化概率（似然）是指的对隐变量训练，这个解析比较明确了。

These models naturally learn high-capacity, overcomplete encodings of the input and do not require regularization for these encodings to be useful.Their encodings are naturally useful because the models were trained to approximately maximize the probability of the training data rather than to copy the input to the output.

调整后：

“这些变种（或衍生）自编码器能够学习出高容量且过完备的模型，进而发现输入数据中有用的结构信息，并且也无需对数据做正则化。 相对于只学习简单恒等函数的自编码器而言，变种（衍生自编码器）产生的编码数据更有效，因为得到的模型是在训练数据集上学习的数据概率分布。”

理由：

这段原文指代感觉比较不清晰，
1：我觉得  capacity、overcomplete 是用来修饰模型的，在前文也是这样使用的，在这句突然用来修饰输入数据的编码 不是太合理。
2：the models were trained to approximately maximize the probability of the training data 说说对这句的理解，感觉隐藏了很多信息。
  译文中“这些模型被训练为近似训练数据的最大概率......” 这句我的理解是 为求解问题构造的目标损失函数是一种概率函数，以最大化概率值为目标。
  而不是产生编码数据的方式是按照近似最大概率的原则产生，因为一旦学习结束，分布就已然得到（通过下文提到的概率分布代入求解），可以直接产生新编码样本点了。因为产生z_mean和z_log_sigma（见相关背景资料）这两个值都是统计量纲，不会有最大化概率这种动作。

  相关背景：

   VAE是个生成模型，三步：
    首先，建立编码网络，将输入映射为隐分布的参数
    然后从这些参数确定的分布中采样，这个样本相当于之前的隐层值
    最后，将采样得到的点映射回去重构原输入。
  由此可知变分编码器的工作原理：
    首先，编码器网络将输入样本x转换为隐空间的两个参数，记作z_mean和z_log_sigma。然后，我们随机从隐藏的正态分布中采样得到数据点z，
    这个隐藏分布我们假设就是产生输入数据的那个分布。z = z_mean + exp(z_log_sigma)*epsilon，epsilon是一个服从正态分布的张量。最后，
    使用解码器网络将隐空间映射到显空间，即将z转换回原来的输入数据空间。
    即：变分编码器不再学习一个恒等的函数，而是学习数据概率分布的一组参数。通过在这个概率分布中采样。
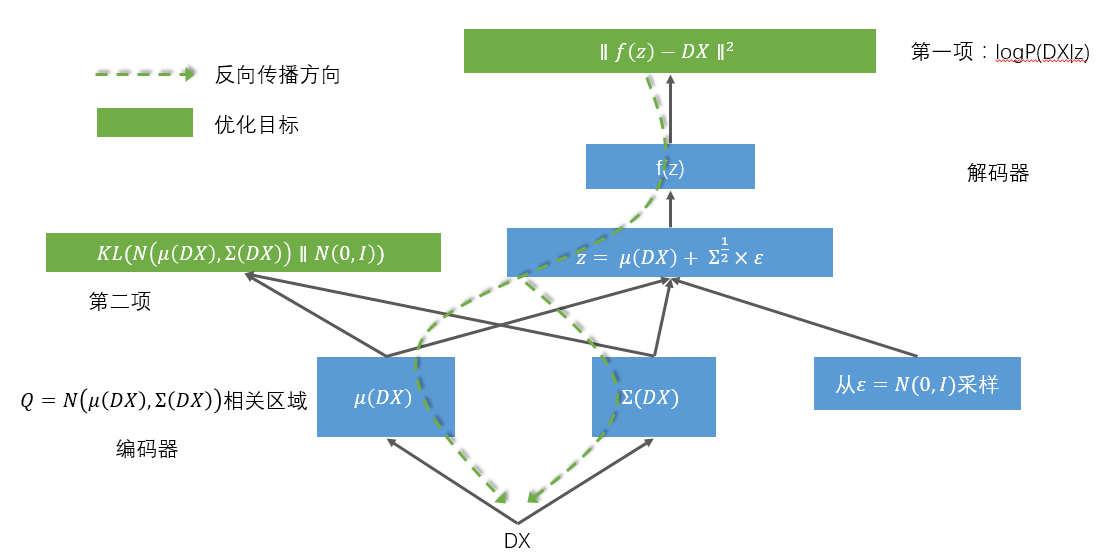
    隐空间参数由两个损失函数来训练，一个是重构损失函数，该函数要求解码出来的样本与输入的样本相似（与之前的自编码器相同），第二项损失函数
    是学习到的隐分布与先验分布的KL距离，作为一个正则。实际上把后面这项损失函数去掉也可以，它对学习符合要求的隐空间和防止过拟合有帮助。

拓扑结构图：

原文 A regularized autoencoder can be nonlinear and overcomplete but still learn something useful about the data distribution even if the model capacity is great enough to learn a trivial identity function

调整后：即使容量足够大的模型去学习一个无意义的恒等函数，非线性和过完备的正则化自编码器仍然能从数据分布中学习到一些有趣的结构，

1：‘模型容量大到足够学习一个简单的复制功能’，让人容易理解为 这个‘简单的复制功能’需要模型足够大才能学习。 2：为啥 a trivial identity function 不翻译为‘无意义的恒等函数’而翻译为‘简单的复制功能’，从机理上说并不是copying（尽管作者大量使用copying task这种术语），更多是学习映射（恒等函数），直译过来感觉让人理解起来不是太精确。 后面‘有用的信息’的表达个人感觉也不够‘达意’，我想真正的表述应该类似”we can discover interesting structure about the data （见UFLDL Autoencoders and Sparsity 一节）应该能点出数据中的某种隐藏的结构。