m
Notation \(m\) clashes with notation \(m\) below.
m
Notation \(m\) clashes with notation \(m\) below.
c
The entry \(2\) should here be \(1\).
α=λ1v1+⋯+λmvm
This should be
$$ \alpha = \lambda_1 y_1 v_1 + \cdots + \lambda_m y_m v_m $$
Notice that \(\beta\) can be found of the binding condition in the primal problem for some \(\lambda_i > 0\).
Differential
Differentiable
zeros.
roots
this translates
Compare this with the limit notation introduced in Chapter 5 below the definition of continuity.
We will assume that there exists α∈Rn\alpha\in \mathbb{R}^nα∈Rn
If this is not the case, the perceptron algorithm will not terminate, but surprisingly it will stay bounded. See Block and Levin, "On the Boundedness of an Iterative Procedure for Solving a System of Linear Inequalities", Proc. Amer. Math. Soc., Vo. 26., No. 2, (1970), 229-245.
There exists \(M\) only dependent on the vectors \(v_1, \dots, v_m\), such that
$$ |\alpha_i| \leq |\alpha_1| + M $$
for every \(i = 1, 2, \dots\). In particular, if the vectors have rational coordinates, the algorithm will eventually cycle.
U
$$ f^{-1}(U) $$
Tak til Christian (Ottosen) for denne rettelse.
d
$$ n $$
Therefore
Consider \(f: \mathbb{R}\rightarrow \mathbb{R}\) given by
$$ f(x) = x^2. $$
Is \(f\) injective? Surjective? Can you adjust the domain and the codomain so that \(f\) becomes bijective?
expressed
You may also view the table form as in the abstract definition of a function
$$ f = {(1, \sqrt{2}), (2, \pi), (3, -1)} \subseteq {1, 2, 3}\times \mathbb{R}. $$
such
Here \(p\) is the logical exclusive or (XOR) function. It is usually denoted
$$ p(x, y) = x \oplus y. $$
composition
Later it will become important that function composition is associative i.e.,
$$ f\circ( g\circ h) = (f \circ g) \circ h $$
whenever these compositions are well defined.
present
Try to do binary search in a natural way in the tree for recovering the classical approximation \(22/7\) for \(\pi\). Here you actually need to descend to more than depth \(10\) in the tree!
The famous approximation \(355/113\) is above depth \(25\).
satsified
satisfied
a proof
Please do check out The Natural Number Game at
https://www.ma.imperial.ac.uk/~buzzard/xena/natural_number_game/index2.html
Here you can see LEAN in action with every step of a proof spelled out!
q2q_2q2
Her skal der stå \(q_3\).
system
Begin by putting
$$ \texttt{left} = \frac{0}{1}\quad\texttt{mediant} = \frac{1}{1}\quad\texttt{right}=\frac{1}{0}. $$
If you move left, keep \(\texttt{left}\), put \(\texttt{right}\) equal to \(\texttt{mediant}\) and compute new \(\texttt{mediant}\). If you move right keep the \(\texttt{right}\) etc.
define
Suppose \(x \neq 0\). Why is \(x^2 > 0\)?
represents
Here the everyday negative number \(-0.8\) is represented as
$$ -1.20000\dots $$
We could also have used a signed model, where \(\sigma = \pm 1\) was added to the representation. This would make the model agree with everyday notation.
a+dc=bdad+bc
You can deduce this formula for addition by using the identity
$$ b d \left(\frac{a}{b} + \frac{c}{d}\right) = a d + b c. $$
21+32=2+31+2=53.
For this formula for addition to make sense, we should have
$$ \frac{1}{2} + \frac{2}{3} = \frac{3}{5} \quad\ = \quad \frac{2}{4} + \frac{2}{3} = \frac{4}{7}. $$
by replacing \(\frac{1}{2}\) by \(\frac{2}{4}\). According to Definition 1.8 it is not true that \(\frac{3}{5} = \frac{4}{7}\).
If v∈V(Jr)v\in V(J_r)v∈V(Jr), then vvv has to be a pole for rrr.
Perhaps clearer: $$ v\not\in V(J_r) \iff r \text{ is defined at } v $$
subsets
open
addition
En god anvendelse her er i tilfældet, hvor bibetingelserne i \(C\) er lineære. Så kan man teste om \(v_0\) er en optimal løsning ved at løse det lineære optimeringsproblem.
$$ \min \nabla f(v_0) v $$
for \(v\in C\). Hvis den optimale værdi er \(\geq \nabla f(v_0) v_0\), så er \(v_0\) en optimal løsning.
These are optimization problems, where C⊆RnC\subseteq \mathbb{R}^nC⊆Rn is a convex subset and f:C→Rf:C\rightarrow \mathbb{R}f:C→R a convex function
Implicit definition af et konvekst optimeringsproblem.
A point v0v_0v0
A critical point
saddle point
Et saddelpunkt antages at være kritisk til at begynde med. Eksemplet
$$ f(x, y, z) = x^2 - y^2 + z $$
har \( (0,0,0)\) som saddelpunkt i henhold til definitionen. Dette punkt er ikke kritisk!
indefinite
Præcise kriterier for hvorrnår en diagonalmatrix er indefinit bør nævnes.
computational graph
With more than 2 edges!
0
\(\mathbb{R}\)
v
Skal være \(u\)
interior
Sød lille opgave: Vis at \(S^o\) er åben.
x0
Mangler transponering
demonstrably false
More precisely \(q\equiv f\). Typically \(q = r \land \neg r\) for some proposition \(r\).
above example
Lidt sjov i gaden. Under forelæsningen spurgte jeg ChatGPT om en formel for summen
$$ 1^3 + 2^3 + \cdots + n^3 $$
hvortil den svarede
$$ \left(\cfrac{n (n+1)}{2}\right)^2 $$
Her virker induktion på samme måde og den distributive lov bruges ved at sætte \((n+1)^2\) udenfor en parentes.
{2,3,8,9}
Her mangler \(C=\)
sloppily
Notice also that \(\mathbb{Z}^2\) (and \(\mathbb{R}^2\) ) is not defined at this point. See below (section 1.6.6).
p1⟺p2
As pointed out by a careful listener during the lecture, this is important. If backtracking to only \(p_2\) we cannot pinpoint that \(p_1\) is false.
compute truth tables
ChatGPT is quite useful here:
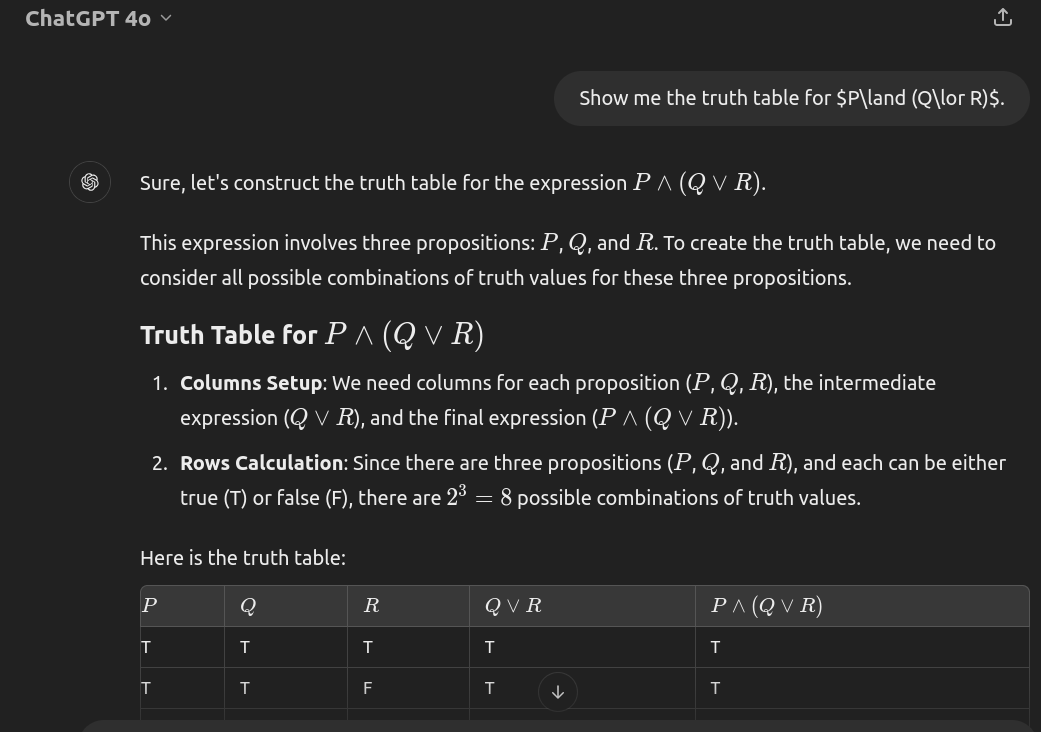
rewrite
Notice that \(\implies\) in the chain of arguments implies that a solution is unique!
another
In a sense you are solving linear equations here by coming up with the clever Lagrange polynomials.
remembers it
Well the new OpenAI model o1 does:
example
Here is another example:
Thanks for asking for yet another example during the lecture.
for
\(\geq\) not defined here
following
Here \(x_1\land (x_2\lor x_3)\) displays as a right answer, but it is wrong.
excerpt
Empty set not defined here.
RP/IP=
Hmmm. It seems that
$$ \frac{\lambda}{g} \equiv \frac{\lambda}{g(3)} \pmod{x-3}, $$
where \(\lambda\in \mathbb{C}\).
slick
In general $$ f\in \sqrt{J} \iff J + (1 - t f) = K[x_1, \dots, x_n, t]. $$
\(\implies\) is proved using the familiar identity $$ \frac{1-a^n}{1-a} = 1 + a + a^2 + \cdots + a^{n-1}. $$
consectetur
NEJ! Annoteringer skal ikke laves i Public gruppen. De skal laves i IMO23 gruppen!
rank 202020.
Nope. The world record is rank >= 28.
this implies
Why is this?
Induced topology
Closure of a subset \(Y\subset X\) is denoted \(\overline{Y}\). It is the intersection of the closed subsets containing \(Y\). If
$$ X = U_1 \cup \cdots \cup U_n $$
is an open cover, then
$$ \overline{Y} = \overline{Y\cap U_1} \cup \cdots \cup \overline{Y\cap U_n}, $$
where \(\overline{Y\cap U_i}\subseteq U_i\) denotes closure in the induced topology.
quotient topology
Consider \(X = [0, 1]\) and \(\sim\) with \(0\sim 1\) and \(x\sim x\) for \(x\in X\). Show that $$ \pi([0, \frac{1}{2})) \subset X/\sim $$ is not an open subset.
g
t
π−1(π(U))=⋃h∈HUh
Er det nu rigtigt? At \(G\rightarrow G/H\) er åben?
positive definite
Extra. Show that a positive definite matrix \(A\) is invertible and that \(A^{-1}\) is positive definite.
result.
Corollary tag missing.
why
Here we may also use Corollary 7.14 (in the textbook) for \(f(x) = x^3\) on \((-\infty, 0)\) and \((0, \infty)\) and then handle the separate cases by hand.
how
Use the trick $$ f = \left(\frac{f}{g}\right) g $$ and then apply the product rule.
by hand
Also, check this using the Sage window after Example 7.7 by doing the appropriate modifications.
beautiful identities
Se
clever statement
Exercise 5.31 kan være nyttig her (specielt første del med infimum).
Show
Definitionen af infimum siger i dette tilfælde at der for alle \(\epsilon >0\) findes \(x_n\) med $$ x_n < \text{inf} + \epsilon \iff x_n - \text{inf} < \epsilon. $$
precise way
Indrømmet. Denne defintion er pebret og kræver tilvænning. En god første ide er helt præcist at benytte definitionen til i detaljer at vise $$ \lim_{n\to\infty} \frac{1}{n} = 0. $$
series
sequence not series
finitely
Faktisk gælder dette også for uendeligt mange lukkede mængder. Det interessant i denne forbindelse er at foreningsmængden
$$ F_1\cup F_2\cup \cdots \cup F_n $$
er lukket.
preimage
Et eksempel: For \(f(x) = x^2\) er
$$ f^{-1}([0,1]) = [-1, 1]. $$
famous result
Læg mærke til den helt naturlige algoritme for at finde nulpunktet \(x_0\): Først sættes
$$ c = \dfrac{a+b}{2} $$
Hvis \(f(c)=0\) er vi færdige. Hvis \(f(c) < 0\) rykker vi venstre endepunkt og sætter \(a = c\) og fortsætter med gennemsnittet ovenfor.
Hvis \(f(c) > 0\) rykker vi højre endepunkt og sætter \(b = c\) og fortsætter med gennemsnittet ovenfor.
Denne algoritme kaldes bisektionsmetoden, da den hver gang halverer længden af intervallet \([a, b]\).
that
I forelæsningerne viste vi også $$ |\lambda v| = |\lambda| |v|. $$
convergent sequence
I forelæsningen så vi hvordan identiteten
$$ \sqrt{2} = 1 + \sqrt{2} - 1 $$
ledte frem til identiteten
$$ \sqrt{2} = 1 + \dfrac{1}{1 + \sqrt{2}} $$
som så førte til en konvergent følge af brøker med grænseværdi \(\sqrt{2}\):
$$ 1, \frac{3}{2}, \frac{7}{5}, \frac{17}{12},\dots $$
completely precise
I forelæsningen talte vi om uendelige decimaltal (decimalbrøker) som model for de reelle tal. Her skal man passe lidt på, da f.eks.
$$ 0.99999\dots = 1 $$
and
Do this also for
a
any
invertible
Lille ekstra opgave: Lad \(A\) og \(B\) være to \(n\times n\) matricer, hvor \(A\) antages at være invertibel. Vis at \(B\) er invertibel hvis og kun hvis \(A B\) er invertibel.
Til forelæsningerne berørte vi hvornår en diagonalmatrix var invertibel. Kan du huske hvad betingelsen var her?
matrix
Lader ikke til at matricer vises korrekt i LaTeX i annotationerne (tak til Andreas for denne observation). Eksempel:\begin{pmatrix} 1 & 0\\ 0 & 1 \end{pmatrix} vises som $$ \begin{pmatrix} 1 & 0\ 0 & 1 \end{pmatrix}. $$
numpy
Under forelæsningerne så vi at numpy gik i skoven i eksemplet med 3x3 matricen [[1, 2, 3], [4, 5, 6], [7, 8, 9]]. Denne matrix er ikke invertibel, men numpy returnerer en invers matrix pga afrundingsfejl.
following
Læg mærke til at dette også kan bruges til at afgøre om en matrix ikke er invertibel: Hvis \(A\) er invertibel og \(A v = 0\) så medfører det at \(v=0\). En invertibel matrix kan ikke sende en vektor forskellig fra \(0\) til \(0\).
answer
Overvej at benytte logaritmen med grundtal \(2\) og uligheden
$$ 2^n n < n! $$
for \(n>5\).
precise proof
Der er her tale om et bevis med ord og forklaringer uden brug af implikationspile som \(\implies\) og \(\iff\). Du er velkommen til i din opgaveløsning at bruge pilene, som er defineret længere nede i teksten.
New York Times
Se også
https://www.nytimes.com/2019/08/21/science/math-equation-triangles-pemdas.html
modern mathematics
Vel ikke alt for moderne? Her en formel: $$ \int_{-\infty}^\infty e^{-x^2} d x = \sqrt{\pi} $$
determinanten
Uddyb determinanten!
-funktioner og proof
Hvad er proof of work?
nspiration til det supplerende
Hvad betyder dette?
equations
What du you mean? Is it not cleat that \(x^2+y^2 = z^2\). Or in display $$ x^3 + y^3 = z^3 $$
f1=200
Tilføjelse per 27/11.
Kommentarer/spørgsmål?
Skulle denne video have været længere og indeholdt feks Lagrangeinterpolation?
Kommentarer/spørgsmål?
Er det ikke for kompliceret?
Kommentarer/spørgsmål?
Her betaler det sig måske at tegne den retvinklede trekant med hypotenuselængde 1.
50.000 år.
Er det ikke lidt af en overdrivelse. Her mangler en kildeangivelse!