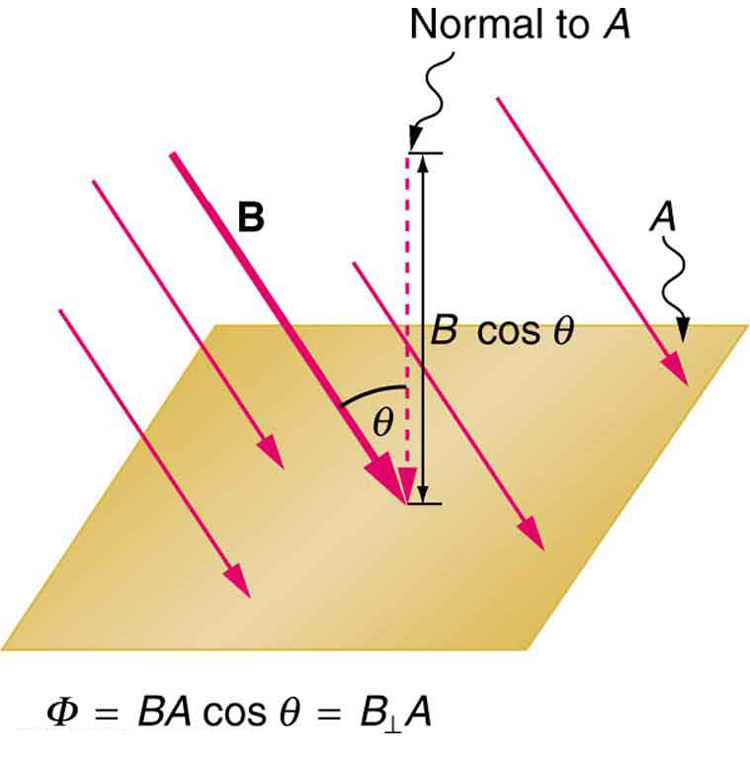
where is the magnetic field strength over an area , at an angle with the perpendicular to the area as shown in Figure 4.
Flux is a fancy way of counting field lines cutting through a given area.
where is the magnetic field strength over an area , at an angle with the perpendicular to the area as shown in Figure 4.
Flux is a fancy way of counting field lines cutting through a given area.
by these rules:
Very important, especially when we get to the topic of flux.
radiation
Not electromagnetic radiation, per se, but charged particles, the protons, electrons and other ions that get lofted from the surface of the Sun, sometimes explosively so.
Explain the importance of the time constant, ,
We will tackle this calculus problem using a spreadsheet method, as we have before!
Voltage is similar to fluid pressure. The voltage source is like a pump, creating a pressure difference, causing current—the flow of charge. The resistor is like a pipe that reduces pressure and limits flow because of its resistance.
A handy analogy. Think of resistance like a load of gravel in a water pipe. Water flows, but not so plentifully as in an empty pipe.
shock wave moves through the system at nearly the speed of light.
Here is the answer to the riddle, drift speed very small, but lights go on almost instantly.
PhET Explorations: Capacitor Lab
Here is the link,
https://phet.colorado.edu/sims/html/capacitor-lab-basics/latest/capacitor-lab-basics_all.html
water molecules gather ions much more effectively because they have an electric field and a separation of charge to attract charges of both signs.
I,=.e., a good solvent
9: The naturally occurring charge on the ground on a fine day out in the open country is . (a) What is the electric field relative to ground at a height of 3.00 m? (b) Calculate the electric potential at this height. (c) Sketch electric field and equipotential lines for this scenario.
A nice workout.
calculate it
There seem to be some typos in the equations below this point. I will try to mend them.
electron–antielectron pai
Yes, we discussed the Feynman diagram for this process in lecture on 6/23/25.
Solving for the position
Similar to $$y\left(t\right)=y\left(0\right)+v_y\left(0\right)t+\tfrac{1}{2}gt^2$$
Constant Acceleration
This is basically a "sideways" gravitational system, \(U_1\left(x\right)=\kappa\,x\) as compared to regular gravitational potential energy, \(U\left(y\right)=\gamma\,y\).
$$\kappa=-E/x_0$$ and $$\gamma=-mg$$
If horizontal gravity DID exist, it would be something like \(U_1\)
an arbitrary direction by d→l,dl→,d\mathbf{\overset{\to }{l}}, so
Similar to my notation, \(d\vec{s}\).
Figure and Figure
ambiguous :(
Substitute
That is a method of pain.
It is better just to know that 1. if \(F\left(x\right)=m\ddot{x}\left(t\right)=-kx\), then \(x\left(t\right)\) is sinusoidal in time, \(x\left(t\right)=A\sin\left(\omega t\right)\) or \(A\cos\left(\omega t\right)\) 2. alternatively, if \(U\left(x\right)=\tfrac{1}{2}kx^2\text{ then }F\left(x\right)=-\frac{d}{dx}U\left(x\right)=-kx\), so \(x\left(t\right)\) is sinusoidal etc.
Then go from there.
Sinusoidal Oscillations
One of the most important examples in the entire book.
can oscillate
Even though it is not exactly a \(\tfrac{1}{2}kx^2\) potential.
Quartic and Quadratic Potential Energy Diagram
Sometimes known as a "sombrero potential" in quantum field theory.

Sometimes, this expression is more convenient to use
Especially when thinking about 1. oscillators and 2. various field like the electromagnetic field.
A 75.0-kg person walks down the central aisle of a subway car
A famous type of example. Einstein wrote his first papers on relativity with explanations of street cars moving at various speeds relative to an observer on the sidewalk. 🙂
displacement from the spring’s unstretched (equilibrium) position
Frequently, we have the freedom to assign the origin to that equilibrium position \(\vec{x}_{eq}\) so that \(\Delta\vec{x}\longrightarrow x\) and \(\vec{F}=\left(-kx\right)\,\hat{i}\).
if they are, they cancel one another
E.g., a spring laid out horizontally on a smooth tabletop, so smooth we can neglect friction for small amplitude experiments. The other forces are downward weight force,
$$\vec{W}=\left(mg\right)\hat{j},\quad g=-9.8\tfrac{m}{s^2}$$,
and the upward normal force \(\vec{N}\) from the rigidity of the surface, which exactly balances the weight force.
Wgrav,AB=−mg^j⋅(→rB−→rA)=−mg(yB−yA).Wgrav,AB=−mgj^⋅(r→B−r→A)=−mg(yB−yA).
Important. If initial point A is above final point B, then (yB - yA) is negative and the product -mg(yB-yA), is positive....it uses the author's g value, 9.8 m/s^2. This means the object gains energy as it falls, kinetic energy.
foot-pound (ft⋅lb).(ft⋅lb).
You occasionally see commodities and machines rated in foot-pounds.
component acting parallel to the other component
In our case, the component of the force acting parallel to the path, \(F_{\parallel}\)
complete understanding of an object’s motion
Momentum and energy are part of the four-dimensional vector that completely encodes an object's dynamics: $$\mathbb{P}= \begin{bmatrix} E/c \ p_x \p_y \ p_z
\end{bmatrix}$$ c = speed of light. This vector is known as the four-momentum and the energy-momentum four-vector.
This impulse is equal to the object’s change of momentum.
Useful non-calculus shorthand: \(\vec{F}_{net}\Delta t =\Delta\vec{p}\)
the rate of change of the momentum that the force causes.
I.e., \(\vec{F}_{net}=\frac{d\vec{p}}{dt}\)
Figure 9.13
The grip is wrong in this diagram, by about \(90^{\circ}\). Do you verify?
Equations of Motion for Uniform Circular Motion
We will lecture on this on 2/7/25
for small angles (less than about ), ( and differ by about 1% or less at smaller angles).
The famous small angle approximation. See, for instance, "Trig function series."
The free-body diagram shows the vertical and horizontal forces acting on the traffic light.
I like this way of diagramming the set of x- and y-components. : )
The large horizontal components are in opposite directions and cancel,
A pattern
Note that the vertical tension in the wire acts as a normal force
I never use the term "normal force" in this manner, because there is no surface in this example. But the textbook author uses the term this way, so take it with a grain of force.
Solution for (a)
Slightly different strategy than what I use: * calculate rise time to apogee, using \(v_y\left(0\right)\); * calculate y-coordinate of apogee; * figure out the drop distance on the downhill side of the arc; * figure out the drop time from apogee to landing point;
This method avoids the big nasty quadratic formula, but you can surely use quadratic formula. : )
Note: in this problem, the rise time (from volcano to apogee) is shorter than the drop time, because the total arc is not symmetric.
Can a goalkeeper
Good exercise
An arrow is shot from a height of 1.5 m toward a cliff of height
Reverse of the "baseball from the top of a cliff" example. I..e., it STARTS at the bottom of the cliff. Key time = 4.0 s.
How many meters lower will its surface be 32.0 km from the ship along a horizontal line parallel to the surface at the ship?
WHOA. Very intriguing!
The cannon on a battleship
Hmmmm. I am intrigued by this one. :D
it is caught at the same height as it left his hand.
home run problem
the bull’s-eye of the target is at same height as the release height of the arrow
home run problem
the top of the takeoff ramp is at the same height as the bus tops
This makes it a "home run" type of problem, i.e., using the symmetries of the ballistic arc that launches and lands at the same y-coordinate.
vertical
I never use the equation involving \(v_{0y}^2 \) and \(v_y^2\), because they are best to study in relation to energy and momentum concepts in later chapter. You can do all projectile problems without it, so THINK carefully.
3: Describe a situation in which one system exerts a force on another and, as a consequence, experiences a force that is equal in magnitude and opposite in direction. Which of Newton’s laws of motion apply?
We will discuss this in lecture on Monday, Aug. 19.
they are internal
This distinction -- internal vs. external -- will be important when we take a peek at atoms.
an acceleration
...an acceleration of the professor and the cart of equipment at the same rate.
Birds and airplanes also fly by exerting force on air in a direction opposite to that of whatever force they need. For example, the wings of a bird force air downward and backward in order to get lift and move forward.
This is an alternate description of the idea of dynamic lift. The usual description of dynamic lift involves a pressure differential in the surrounding fluid, air, due to the Bernoulli Effect.
loosely
In the energy-momentum method for studying the dynamics of a system, later in this textbook, we will find a perfect quantity that encodes the interaction equally, so that "action-reaction" is no longer a loose usage.
complicated mechanism
An understatement.
For example, let’s compare the motions of two baseballs. One baseball is dropped from rest.
Similar to a Ferrari going off a cliff, a problem that has been on midterms in previous semesters.

Although varies from to , depending on latitude, altitude, underlying geological formations
This kind of variation is how petroleum geologists discovered the Chicxulub impact crater in the Yucatan and Gulf of Mexico. This asteroid/comet impact is what scientists now believe triggered the extinction of most dinosaurs.
the average value
Be aware.
The textbook uses \(g=9.80\,m/s^2\) for the acceleration due to gravity at the surface of Earth. I, however, prefer to encode the direction with a - sign, $$g=-9.8\frac{m}{s^2}$$
A vector is any quantity with both magnitude and direction.
The definitive vector is the velocity vector, also defined as a tangent vector especially when working in four dimensional spacetime.

Greek letter (delta) always means “change in”
D for \(\Delta\), D for difference, i.e., subtraction.
sells bags of apples
Labeled as "5 lbs," so that is like the notional value "45000 miles" in the previous example.
they are each rather close to the actual location
If you were at a rifle range, sighting in your hunting gear, then you'd say, "Yes, I am inside the first ring, but that would not be good enough unless I am shooting the side of a barn." So maybe you adjust the magnification of your optics or buy a new sight with better optics.... or keep practicing!
rather far away from the actual location of the restaurant
So, if you were at a rifle range, you'd want to adjust your sights slightly, to get that group up and to the right, into the center.
“known masses”
The metric system is based on cubic centimeters (cc) of liquid \(H_2O\). Balance the object you are measuring with a number of cc's of liquid water, that will tell you the number of grams in your object. That is the theory. In practice, yes, you'd use various carefully machined metal cylinders etc.

observation and experiment
A famous dictum, ascribed to Galileo, is
"Measure what is measurable, and make measurable what is not so."
Perform unit conversions both in the SI and English units Explain the most common prefixes in the SI units and be able to write them in scientific notation
Good to review and double-check from time to time during the semester.
must be used for objects smaller than can be seen with a microscope.
Where Planck's constant, \(\hbar=6.58\times 10^{-16}\,eV\,s\) rules all, in which the wave properties of matter are significant.
Relativity must be used whenever an object is traveling at greater than about 1% of the speed of light or experiences a strong gravitational field such as that near the Sun.
Systematic explication of how four-dimensional spacetime behaves under various energy conditions, how four dimensional spacetime curves and affects various forms of energy, and all because of the nature of LIGHT. \(E=mc^2\) is just one equation from the most basic relativity ideas.
mystery, imagination, struggle, triumph, and disappointment
"Drama" :D
membranes.
Electrical structures. You will learn this in PHY2054.
It is not necessary to formally study all applications of physics. What is most useful is knowledge of the basic laws of physics and a skill in the analytical methods for applying them.
An enormous statement. It emphasizes what scientists do: figure out new things, by putting together a framework from first principles. That is problem-solving, which is what we want to be able to do on PHY2053/4.
from one location to another
And because GPS, of necessity, uses Einstein's general theory of relativity, even though the spacetime curvature in the neighborhood of Earth is so tiny, the civilian GPS in your vehicle can locate your vehicle to within a few feet almost anywhere on Earth. Without relativity, GPS would not be nearly as precise.
you will gain analytical abilities
I.e., learn to THINK.
broadly applicable physical laws, permitting an understanding beyond just the memorization of lists of facts.
This is why studying for a physics class is different from a class where memorization is of paramount importance, like an anatomy class.
as food calories, batteries, heat, light, and watch springs
...as well as the theory of currved four-dimensional spacetime, Einstein's general theory of relativity.

quarks
Sub-nuclear particles that bind together to form protons and neutrons plus other exotic subatomic particles like the \(\pi^+\) meson.
An RLC circuit
A nice simulator for RLC and RC and LC circuits.
Try
Worth fooling around with this one.
angular frequency of the oscillations
Derived in lecture on 11/15
we obtain
Here is the precise combination in terms of \(R\), \(L\), and \(C\).
Damped oscillations of the capacitor charge are shown in this curve of charge versus time, or q versus t. The capacitor contains a charge q0q0{q}_{0} before the switch is closed
Discharge curve, a combination of real exponential \(e^{-\alpha t}\times\) complex exponentials \(e^{\pm i\omega t}\)
Ey(x,t)=E0cos(kx−ωt).Ey(x,t)=E0cos(kx−ωt).{E}_{y}\left(x,t\right)={E}_{0}\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}\left(kx-\omega t\right).
Phase \(\phi=kx-\omega t\)
Phase \(\phi=0\) corresponds to the first peak of the \(E_y\) field; \(\phi=2\pi\) corresponds to second peak, and so on. This means that the equation \(kx-\omega t=0\) is the equation of motion for the first peak of the wave, the "wave top" of the wave. Another way to view this is that
$$x=\frac{\omega}{k}t$$
That factor \(\frac{\omega}{k}\) must be the same as \(c\), the speed of the light wave.
Fourier’s theorem
Fourier transforms, another huge tool
This is the form taken by the general wave equation for our plane wave.
This concludes the derivation of the wave equation for electromagnetic waves, specifically for \(E_y\left(t,x\right)\). The constants \(\epsilon_0\text{ and }\mu_0\) are related therefore to the speed of light, \(c\).
we can set Qin=0Qin=0{Q}_{\text{in}}=0 and I=0I=0I=0 in Maxwell’s equations
a.k.a. the vacuum solutions
beyond the scope of this textbook.
Understatement. It is a lifetime's study, and that would only be scratching the surface.
do not require a medium for their propagation.
i.e., only a vacuum is needed.
through space
Even through a vacuum
interference patterns
Here is a nice blurb in YouTube about interference patterns. It is a HUGE tool for physicists and engineers. https://youtu.be/D7aftTF--5w?si=hABIsE089aUZpVT0
propagate through space.
A nice diagram
This unification of forces has been one motivation for attempts to unify all of the four basic forces in nature—the gravitational, electrical, strong, and weak nuclear forces
Einstein's great quest, but he died before he reached it, and, in fact, no one has reached it yet.
contains a charge q0q0{q}_{0} before the switch is closed
Initial condition: Charged up, i.e., \(q\left(0\right)=q_0\)
the electromagnetic energy of the oscillating circuit
Nice exercise
initial energy of the system
I.e., initial load in the capacitor
what is C
plug-in exercise
How long does it take the capacitor to become completely discharged?
Good exercise
The time variations of q and I
It is interesting to normalize the total energy equation to 1 by dividing both sides by U -- should result in a version of the Pythagorean Identity \(\sin^2\left(x\right)+\cos^2\left(x\right)=1\)
Joule heating
Joule heating, for which the energy dissipation rate is \(P=I^2 R\), and which is also known as "\(I^2 R\) heating."
Since there is no resistance in the circuit
idealization
all the energy is stored in the magnetic field of the inductor
Similar to a spring system at equilibrium, \(x=0\), where kinetic energy
$$\frac{1}{2}m\dot{x}^2$$
is maximum.
This energy is
If you think of the charge \(q\left(t\right)\) as a coordinate, e.g., like \(x\left(t\right)\), then \(U_C\) is like the potential energy of a spring oscillator,
$$U=\frac{1}{2}kx^2$$
but for which the spring constant is \(1/C\)
the total energy U in the circuit is given by
Resembles another famous system,
$$E=\frac{1}{2}kx^2+\frac{1}{2}m\dot{x}^2$$
the harmonic oscillator.
With the substitution of Equation 14.14, this becomes U=12LI2.U=12LI2.U=\frac{1}{2}L{I}^{2}. Although derived for a special case, this equation gives the energy stored in the magnetic field of any inductor.
Quadratic in current \(I\), therefore current \(I\) will oscillate.
velocity selector
We will review this application in lecture
0.5-mm segment
Note that the diagram here and Fig. 12.3, greatly exaggerate the length of the line element \(d\vec{\ell}\)
The diagram in Webcourses is much more accurate.
If not
A big "if" with a ton of trig involved.
Since the current segment is much smaller than the distance x
Since \(x\gg\ell\), the approximation as \(\Delta\ell\) is good, and so is the approximation \(r_p\approx x\)
A 10-A current flows through the wire shown.
Homework problem
You might expect that two current-carrying wires
We will tackle this section and 12.1 Biot Savart Law on Monday, Nov. 6 Biot-Savart is ROUGH.
The component of the velocity perpendicular to the magnetic field produces a magnetic force perpendicular to both this velocity and the field: vperp=vsinθ,vpara=vcosθ.vperp=vsinθ,vpara=vcosθ.{v}_{\text{perp}}=v\phantom{\rule{0.1em}{0ex}}\text{sin}\phantom{\rule{0.1em}{0ex}}\theta ,\phantom{\rule{0.5em}{0ex}}{v}_{\text{para}}=v\text{cos}\phantom{\rule{0.1em}{0ex}}\theta . where θθ\theta is the angle between v and B.
Needs a diagram!!!!!! A 3-D blackboard is needed here.
following figure
heinous diagram
circular motion of the charged particle
Because \(\vec{F}\text{ is always }\perp \vec{v}\)
A magnetic field is defined by the force that a charged particle experiences moving in this field,
Operational or experimental definition, but not a theoretical definition!
The compass needle near the wire experiences a force that aligns the needle tangent to a circle around the wire.
What the observer sees: the compass needle aligns to the field. Lecture, 10/23
What is the average
I am not sure why this problem is here.
To form a hydrogen atom
Good. Be sure to verify this answer.
If Q3Q3{Q}_{3} starts from rest
Technically, this makes the problem insoluble, since it is not specified that \(Q_1\) and \(Q_2\) are static, fixed in place, or not. IF you consider then to be fixed in place, it is an easy problem we have already studied. So proceed on that basis: I may review this problem in lecture on Wednesday, or in Discusssions.
Consider a charge Q1(+5.0μC)Q1(+5.0μC){Q}_{1}\left(+5.0\phantom{\rule{0.2em}{0ex}}\mu \text{C}\right) fixed at a site
A good workout with the nitty gritty of EPE, KE etc.
Is the electrical potential energy of two point charges positive or negative
Significant question. The potential energy curve rules the dynamical world.
* Here is a potential barrier,
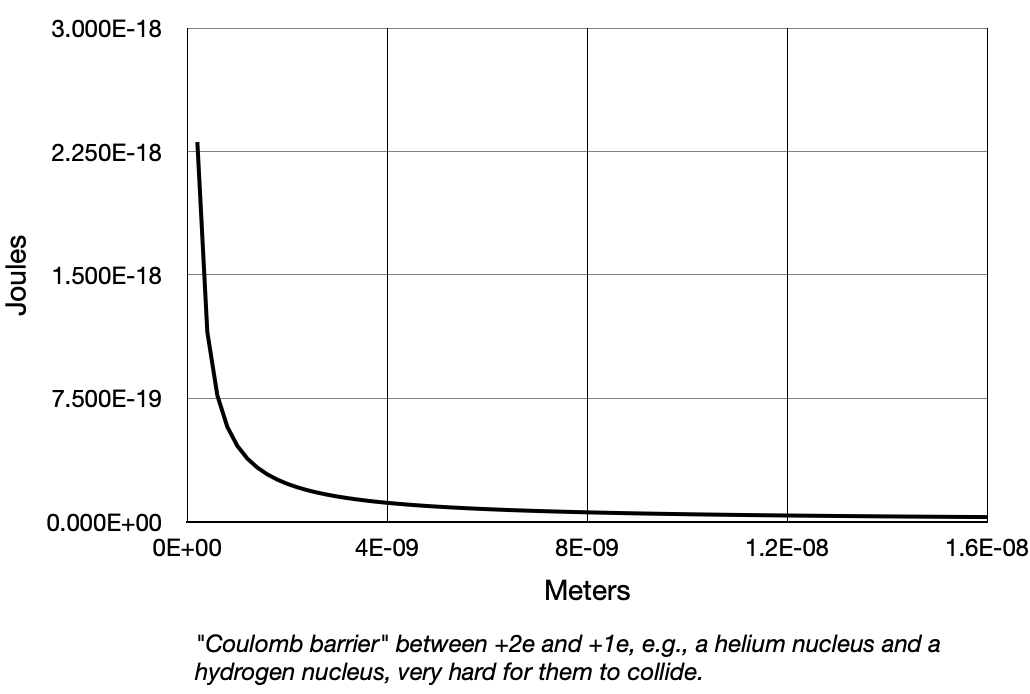 * Here is a potential well.
* Here is a potential well.
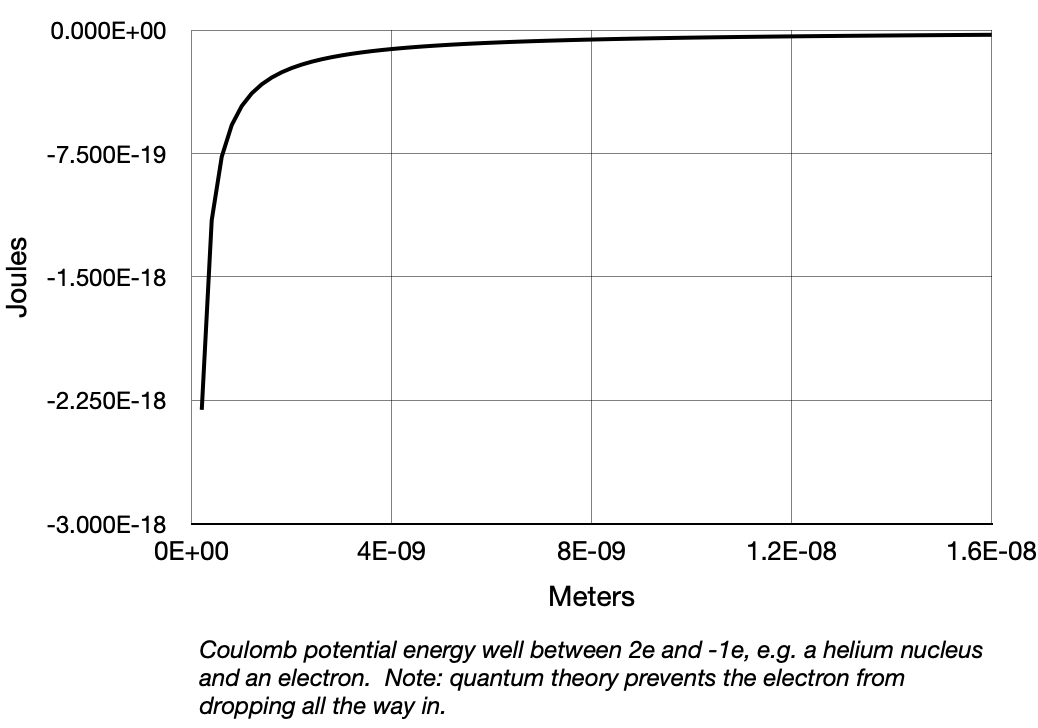
There is a huge difference between them, and the implications extend from quantum electrodynamics to black holes.
Assembling Four Positive Charges
Finish working this one out, and try to follow the logic of the textbook authors. It is slightly different than my description, so understanding both will help you.
all of the potential energy gets converted to kinetic.
"energy at infinity" is all kinetic. The charge Q effectively has no interaction with q.
it is perpendicular to the displacement along these arcs.
As noted in lecture, 10/2
Potential Energy of a Charged Particle
A good problem to work out.
Electric Field between Oppositely Charged Parallel Plates
This diagram and description will be on part 1 of the midterm, one or two multiple choice concept questions
Note that the electric field outside a spherically symmetrical charge distribution is identical to that of a point charge at the center that has a charge equal to the total charge of the spherical charge distribution. This is remarkable since the charges are not located at the center only.
Also a very important result in Newton's Law of Universal Gravitation.
permittivity of free space
$$k=\frac{1}{4\pi\epsilon_0}$$ so $$\epsilon_0 = \frac{1}{4\pi k}$$
This can be directly attributed to the fact that the electric field of a point charge decreases as 1/r21/r21\text{/}{r}^{2} with distance, which just cancels the r2r2{r}^{2} rate of increase of the surface area.
Not a coincidence. The Coulomb interaction is formally an infinite range interaction, directly because it is inverse \(r^2\)
Therefore, we can write the electric flux ΦiΦi{\text{Φ}}_{i} through the area of the ith patch as
Preparing to integrate!
Example
Nice example, very basic
It is positive when the angle between →EiE→i{\stackrel{\to }{\textbf{E}}}_{i} and ^nn^\hat{\textbf{n}} is less than 90°90°90\text{°} and negative when the angle is greater than 90°90°90\text{°}.
$$0^{\circ}\leq\theta\leq 180^{\circ}$$ I.e., from parallel to antiparallel
This estimate of the flux gets better as we decrease the size of the patches.
Here we go. Calculus ahead
similar to the way
Also similar to how CGI makes Gollum from the "wire frame" generated by Andy Serkis' motion capture suit.<br />

On a closed surface such as that of Figure 6.6(b), ^nn^\hat{\textbf{n}} is chosen to be the outward normal at every point
Important
area (A)
Its destiny is to become an element of area, e.g.,
$$dA=dx\, dy$$
or
$$dA=r\,dr\,d\theta$$
N
Unfortunate choice of symbol, because it confounds with the unit of E field, \(\frac{N}{C}\).
(N⋅m2/CN·m2/C\text{N}·{\text{m}}^{2}\text{/C}).
I.e., units of E field, \(\frac{N}{C}\,\,\times\) units of area \(m^2\).
a hula hoop in a flowing river
Even better: a hula hoop held out the window by a friend as you drive up Alafaya to Publix for Chinese food. Even your hand out the window works a bit as an analogy. If your hand is orthogonal to the road and therefore to the velocity of the air rushing past, you feel its force of air resistance. But if you hold your palm flat, parallel to the road surface, you feel way less air resistance.
the number of electric field lines passing through an area
This statement, however, is limited, because the electric field fills ALL of space, so that is a continuous \(\infty\) of vectors, no matter what direction the element of area \(dA\) is oriented.
SO... we must agree upon a standard of field line density, somehow.
the dot product of a vector field (in this chapter, the electric field) with an area.
I.e., $$d\vec{E}\cdot\, \hat{n}\,dA$$, in which \(\hat{n}\) encodes the orientation of the infinitesimal tile of surface, \(dA\)
Electric Field due to a Ring of Charge
Hmmmmmmmmmmmm....... will there be time on Friday in lecture?
Draw the electric field for a system of three particles
Hmmmmmmmm.....
field line density
Flux!
The field line diagram of a dipole.
A ubiqitous diagram, very famous, because many molecules, even large ones, have a polar symmetry: a more positive end and a more negative end. Example: \(H_2O\).
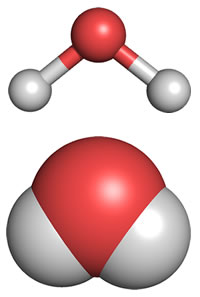
vector field diagram of a dipole
The guts of our Quiz 1
and the vectors →ri=ri^rir→i=rir^i{\stackrel{\to }{\textbf{r}}}_{i}={r}_{i}{\hat{\textbf{r}}}_{i} are the displacements from the position of the ith charge to the position of Q.
Covered in lecture, 8/28/23, in my comments about \(\hat{r}_{21}\)
amber
Where we get the word "electric" and "electron."
it will stick to the wall
Or to your head. :D
put the comb close to a thin stream of water
You can easily do this experiment at home. Kinda cool.
n figure (a), a person holding the spinning bike wheel
We normally do this demonstration in lecture on the first day of the semester.
165 km/h
about 103 mph
without the aid of friction between the tires and the road.
This makes the example more of a pin ball machine: give the object some speed than inject it into the "frictionless" track.
For this formula, it is also interesting to think about the circular proving track in Italy, the Nardo ring. It is banked, unlike this example, but there is still a correspondence between optimum speed \(v\) and the track's turn radius, \(r\). That is because the track surface and tires have a set coefficient of friction, and \(g\) is known, so the turn radius for the speed you want can be calculated:
$$r=\frac{v^2}{\mu_s g}$$
That is,
1. Decide the top speed at which you want to test,
2. then calculate the turn radius you need,
3. and therefore the amount of land you need to build your own test track.

A fairground ride spins its occupants inside a flying saucer-shaped container. If the horizontal circular path the riders follow has an 8.00 m radius, at how many revolutions per minute will the riders be subjected to a centripetal acceleration whose magnitude is 1.50 times that due to gravity?
A good workout, and you can check your answer. If you work through Example 2 (above) then you can definitely work this problem... though they are not identical.

The same force exerted on systems of different masses
Think of this as similar to what we observed with the skateboarder interactions, where the smaller skateboarder got noticeably more speed.
The force exerted by a stretched spring can be used as a standard unit of force.
This is like a sideways version of an old-fashioned spring scale. A modern scale uses a device called a strain gauge or a piezo-electric cell, each of which generates shanges in electrical current based on strain or pressure applied to the device.
A plot of position or of velocity as a function of time can be very useful.
True true true. If you have a velocity graph, you can analyze it for two other important physical quantities: 1. position and distances, which we get by calculating areas. Terms for this calculation are velocity rectangle and velocity triangle. 2. accelerations, which we get by computing slope of the graph, rise over run in geometry class but \(\frac{\Delta\vec{v}}{\Delta t}\) on a velocity graph in physics class.
Sir Isaac Newton himself figured out that position, velocity and acceleration are the main physical quantities a scientist needs to study any moving physical object, and that they all relate directly to his construct, forces.
Problems & Exercises
This section, Ch. 3.4, is the target section for Midterm Exam 1, for Summer B, 2023.
For that reason, these problems and exercises are good good good practice if you are preparing to crush the midterm.
gases are easily compressed, whereas liquids are no
A gas like \(O_2\) molecular oxygen can be converted to a liquid by compressing it. AND, a tank of LOX liquid oxygen has to be kept cold and under pressure, like on the space shuttle, one of the last things loaded before launch.

Moon’s differential attraction
This is a good reinforcement on the lectures about tidal heating in Io and Enceladus.
emission line spectrum
NASA image of several emission spectra:
 *
*
Modeling
Here is a YouTube of a nice standing wave demonstration a few years ago.
Example
This example is slightly deceptive, in that it presumes that the value of \(G\) is already known. Historically, that was not the case. The first successful measurement of the value of \(G\) in the laboratory in 1798, by Prof. Henry Cavendish of Cambridge University, led to a calculation of the density and mass of Earth.
7: Find the direction and magnitude of the force that each wire experiences in Figure 5(a) by, using vector addition.
Brain burner of the century!
Angular Momentum of Three Particles
Another good workout
Calculate the torque
A good workout
To illustrate this
A good illustration.
Three 70-kg deer are standing on a flat 200-kg rock
Good workout that makes you think.
Potential Energy of a Vertical Mass-Spring System
There is an error in this example.
change in elastic potential energy is
Error. \(\left(5.0\, cm\right)=0.05\, m\)
So \(\Delta U_{elastic}\longrightarrow -0.0075\, J\)
an exact differential,
"exact differential" is pertinent to a differential equations course and frequently seen in physical applications for the first time in a thermodynamics course.
SO... this section is the author's way of giving you a sneak preview of something almost every engineering and physics major will eventually see.
21.5 Null Measurements
Bypass
21.4 DC Voltmeters and Ammeters
Optional. Read or skim if you have a personal interest.
Later on, during the eighteenth century, the name kinetic energy was given to energy of motion.
This paragraph distills an enormous amount of history, several century of thinking about quantifying motion, which led us to the idea of \(\frac{1}{2}mv^2\) kinetic energy.
the dot product of these two vectors:
Reminiscent of the impulse formula, $$d\vec{p}=\vec{F}_{net}\Delta t$$ which describes an increment of dynamical change to the momentum of the object, \(\vec{p}\)
a large amount of charge
"a large amount of charge" is nebulous, unless you compare it to something else well known. \(I = 1.00\) Ampere of current flowing for 1.00 second = 1.00 Coulombs. In terms of electrons, that would be much less than 1.00 mole of electrons in motion:
$$I=1.00\frac{C}{s}=\left(\frac{1.00\,C}{1.602\times10^{-19}C/e}\right)/{s}$$
$$I=\left(6.248\times 10^{18}e\right)/s \ll N_{A}/s$$
Meanwhile a calculator might operate with current \(I_2\) of a few micro Amps of current would be even fewer electrons per second.
$$I_2 =\left(6.248\times 10^{12}e\right)/s \ll N_{A}/s$$
So it all depends on what you consider to be "large" or "small."
Banked Curves
A nice example
The final charge placed on a capacitor experiences , since the capacitor now has its full voltage on it. The average voltage on the capacitor during the charging process is , and so the average voltage experienced by the full charge is . Thus
Huge calculus bypassed here, but average voltage etc. does an adequate job for now.
5: Find the total capacitance
A good brain burner!!
4: Find the total capacitanc
A good study problem
Several Forces on a Particle
Nice combo example
Block on the Table (Coupled Blocks)
Another good example of two coupled free body diagrams. What is the force that mediates the coupling of the diagrams?
with force components
Sometimes I sketch the components of a constituent force in the free body diagram itself, and other times I split off a separate diagram of just the constituent force vector, like \(\vec{P}\) here, somewhere off to the side for clarity, and then sketch in its components.
Two Blocks in Contact
I like this example, featuring two free body diagrams that are coupled together by interaction forces \(\vec{A}_{21}\) and \(\vec{A}_{12}\)
In this case, place a squiggly line
Optional. I never do this. But remember that the textbook author DOES use squigglies.
If you are treating the object as a particle (no size or shape and no rotation), represent the object as a point.
This is what we will normally do.
free-body diagram, which is a sketch showing all external forces acting on an object or system. The object or system is represented by a single isolated point (or free body), and only those forces acting on it that originate outside of the object or system—that is, external forces—are shown.
Important definition
11: (a) What is the direction of the total Coulomb force on q
A nice sketching exercise!
magnitude
Be careful with the - signs in this section. :\
The electric field is defined in such a manner that it represents only the charge creating it and is unique at every point in space.
"only the charge creating it" ← those charge are also known as source charges.
John Travoltage
Kind of idiotic but...
Motion of a Motorboat
A good generic example that uses
Rocket Booster
A good brain burner
Vertical Motion of a Baseball
A very good exercise
Free Fall of a Ball
A good exercise
If we define the upward direction as positive, then a=−g=−9.8m/s2,a=−g=−9.8m/s2,a=\text{−}g=-9.8\,{\text{m/s}}^{2}, and if we define the downward direction as positive, then a=g=9.8m/s2a=g=9.8m/s2a=g=9.8\,{\text{m/s}}^{2}.
Here is how the author uses \(g\) so be alert.
let’s use an average value of 9.8 m/s2
Good. And I like to denote its downwardness with a negative sign, $$g=-9.8\frac{m}{s^2}$$ and as a vector, $$\vec{g}=\left(-9.8\frac{m}{s^2}\right)\hat{j}$$
yielding
We will use calculus, not this average velocity argument, to derive \(x\left(t\right)=x\left(0\right)+v_x\left(0\right)t+\frac{1}{2}at^2\)
sail into the wind
...like these guys!

Figure 3.
Notice how the streamlines get crowded together on one side of the airfoil... the lift goes toward those crowded stream lines.
Bernoulli’s equation is a form of the conservation of energy principle.
Good concept to remember. You can see the "remnant" of the conventional kinetic energy fmla in $$\frac{1}{2}\rho v^2$$
and the remnant of gravitational potential energy in $$\rho g h$$
The new term is pressure. When we talk about photons at the end of the semester, it gets even more interesting!
You may also have noticed that when passing a truck on the highway, your car tends to veer toward it.
Cool effect. This is essentially dynamic lift, but working sideways!
Example 3: Calculating Flow Speed and Vessel Diameter: Branching in the Cardiovascular System
Interesting example for all biology students
This is called the equation of continuity
Continuity equation is important. Fig. 2 is good.
This equation seems logical enough.
Actually has to do with the idea of flux, which we will also use in electromagnetism, e.g., a magnetic field flux, Fig. 4, Ch. 23.1
volume of water contained in a 6-lane 50-m lap pool
Amazing