This is very true.
And one reason more why especially palaeontologists should stop ignoring distance-based networks (following the Farris'ian Dogma that "distance = phenetic", but see Felsenstein, 2004, Inferring Phylogenies) as a tool to explore the non-trivial signal in their data sets — some application examples posted at the Genealogical World of Phylogenetic Networks; see also Denk & Grimm, Rev. Pal. Pal. 2009, Bomfleur et al., BMC Evol. Biol. 2015, —, PeerJ, 2017. Even in the absence of reticulation, evolving morphologies do not provide tree-like signal, because synapomorphies, characters fully compatible with the true tree, are rare, homoiologies common, and convergences, characters incompatible with the true tree, inevitable.
The less tree-like the signal and the more different the individual probabilities for change, the more misleading or ambiguous will be the parsimony tree reconstruction. Neighbour-nets may appear to be crude tools, but are quick-to-infer, designed to handle data incompatibility. Consensus networks are, in any possible aspect, more informative than a strict or majority rule consensus tree.
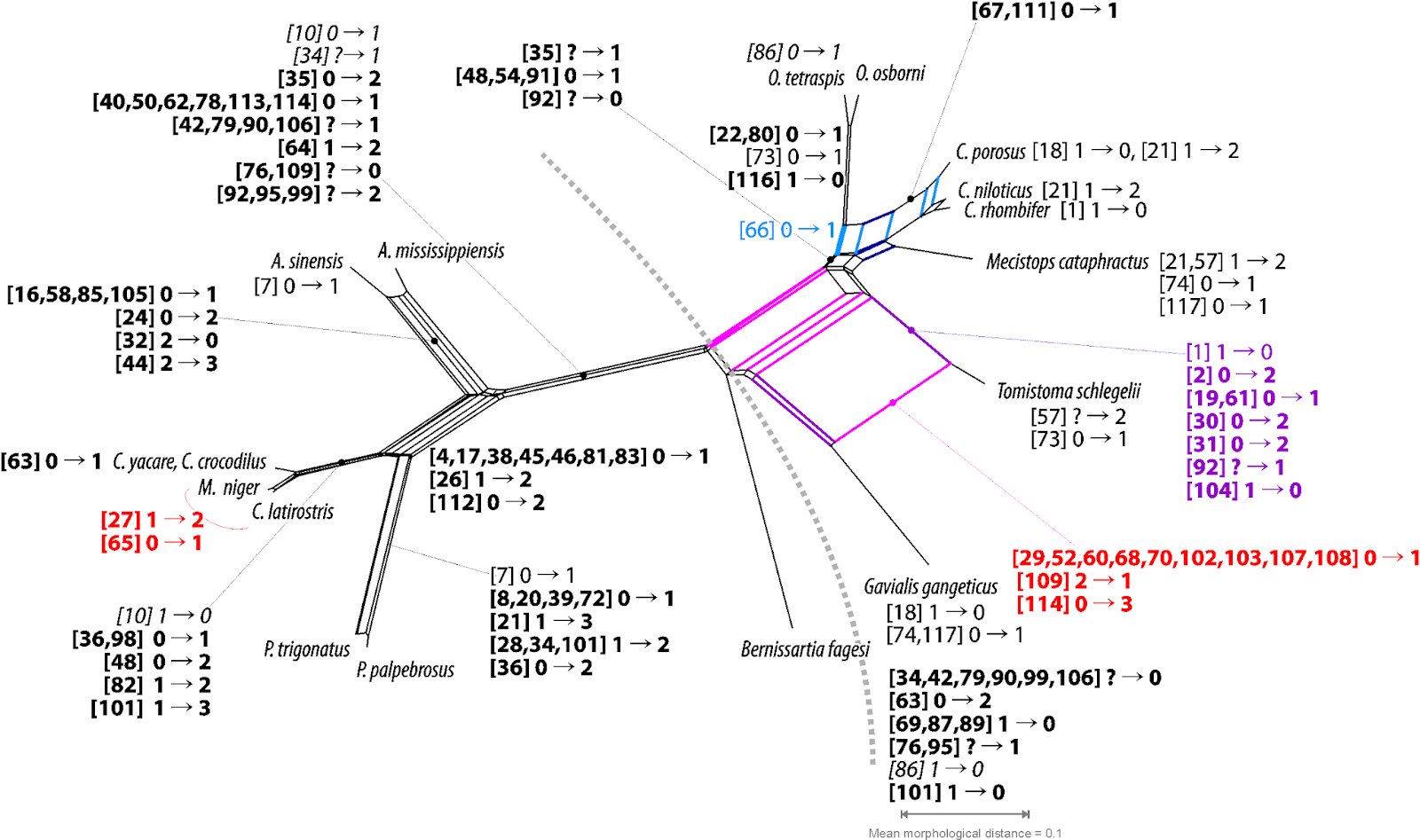
Instead of trying to decide between equally and inevitable biased trees, we can just explore our data, using networks. See pic, depicting all potential synapomorphies, bold, symplesiomorphies, italics, and homoiologies that can be inferred directly from the crocodilian morphomatrix. Naturally including pseudo-synapomorphies (red) when compared to the provided molecular tree.
PS That the way out of the dilemma is to embrace networks has been realised very early in evolutionary sciences (long before Hennig and Farris).

 Vice versa, blue is the symplesiomorphy, pink the homoiology found only in the most derived (in absolute evolutionary terms) taxa
Vice versa, blue is the symplesiomorphy, pink the homoiology found only in the most derived (in absolute evolutionary terms) taxa