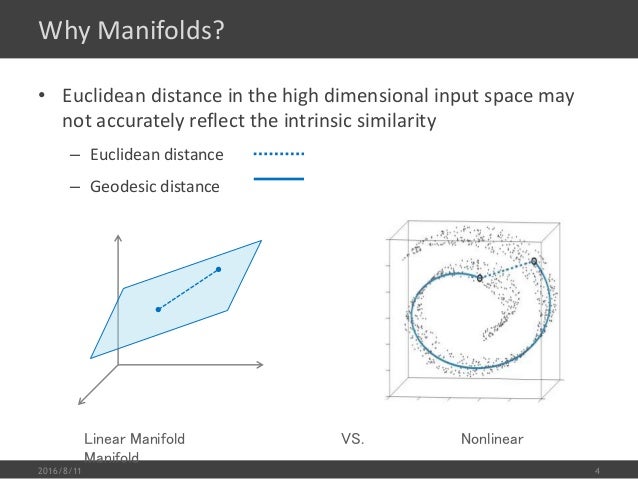
T-distribution Stochastic Neighbor Embedding(t-SNE)

之前介绍的所有方法都存在相同的弊病：

similar data are close, but different data may collapse，亦即，相似（label）的点靠的确实很近，但不相似(label)的点也有可能靠的很近。

t-SNE 的原理

\(x \rightarrow z\)

t-SNE 一样是降维，从 x 向量降维到 z. 但 t-SNE 有一步很独特的标准化步骤：

一， t-SNE 第一步：similarity normalization

这一步假设我们已经知道 similarity 的公式，关于 similarity 的公式在【第四步】单独讨论，因为实在神妙。

这一步是对任意两个点之间的相似度进行标准化，目的是尽量让所有的相似度的度量都处在 [0,1] 之间。你可以把他看做是对相似度进行标准化，也可以看做是为求解KL散度做准备 --- 求条件概率分布。

compute similarity between all pairs of x: \(S(x^i, x^j)\)

我们这里使用 Similarity(A,B) 来近似 P(A and B), 使用 \(\sum_{A\neq B}S(A,B)\) 来近似 P(B)

\(P(A|B) = \frac{P(A\cap B)}{P(B)} = \frac{P(A\cap B)}{\sum_{all\ I\ \neq B}P(I\cap B)}\)

\(P(x^j|x^i)=\frac{S(x^i, x^j)}{\sum_{k\neq i}S(x^i, x^k)}\)

假设我们已经找到了一个 low dimension z-space。我们也就可以计算转换后样本的相似度，进一步计算 \(z^i\) \(z^j\) 的条件概率。

compute similarity between all pairs of z: \(S'(z^i, z^j)\)

\(P(z^j|z^i)=\frac{S(z^i, z^j)}{\sum_{k\neq i}S(z^i, z^k)}\)

Find a set of z making the two distributions as close as possible:

\(L = \sum_{i}KL(P(\star | x^i)||Q(\star | z^i))\)

二， t-SNE 第二部：find z

我们要找到一组转换后的“样本”， 使得转换前后的两组样本集（通过KL-divergence测量）的分布越接近越好：

衡量两个分布的相似度：使用 KL 散度(也叫 Infomation Gain)。KL 散度越小，表示两个概率分布越接近。

\(L = \sum_{i}KL(P(\star | x^i) || Q(\star | z^i))\)

find zi to minimize the L.

这个应该是很好做的，因为只要我们能找到 similarity 的计算公式，我们就能把 KL divergence 转换成关于 zi 的相关公式，然后使用梯度下降法---GD最小化这个式子即可。

三，t-SNE 的弊端

1. 需要计算所有两两pair的相似度
2. 新点加入，需要重新计算他与所有点之间的相似度
3. 由于步骤2导致的后续所有的条件概率\(P\ and\ Q\) 都需要重新计算

因为 t-SNE 要求我们计算数据集的两两点之间的相似度，所以这是一个非常高计算量的算法。同时新数据点的加入会影响整个算法的过程，他会重新计算一遍整个过程，这个是十分不友好的，所以 t-SNE 一般不用于训练过程，仅仅用在可视化中，即便在可视化中也不会仅仅使用 t-SNE，依旧是因为他的超高计算量。

在用 t-SNE 进行可视化的时候，一般先使用 PCA 把几千维度的数据点降维到几十维度，然后再利用 t-SNE 对几十维度的数据进行降维，比如降到2维之后，再plot到平面上。

四，t-SNE 的 similarity 公式

之前说过如果一种 similarity 公式：计算两点(xi, xj)之间的 2-norm distance（欧氏距离）：

\(S(x^i, x^j)=exp(-||x^i - x^j||_2)\)

一般用在 graph 模型中计算 similarity。好处是他可以保证非常相近的点才会让这个 similarity 公式有值，因为 exponential 会使得该公式的结果随着两点距离变大呈指数级下降。

在 t-SNE 之前有一个算法叫做 SNE 在 z-space 和 x-space 都使用这个相似度公式。

similarity of x-space: \(S(x^i, x^j)=exp(-||x^i - x^j||_2)\) similarity of z-space: \(S'(z^i, z^j)=exp(-||z^i - z^j||_2)\)

t-SNE 神妙的地方就在于他在 z-space 上采用另一个公式作为 similarity 公式, 这个公式是 t-distribution 的一种（t 分布有参数可以调，可以调出很多不同的分布）：

\(S(x^i, x^j)=exp(-||x^i - x^j||_2)\) \(S'(z^i, z^j)=\frac{1}{1+||z^i - z^j||_2}\)

可以通过函数图像来理解为什么需要进行这种修正，以及这种修正为什么能保证x-space原来近的点, 在 z-space 依旧近，原来 x-space 稍远的点，在 z-space 会拉的非常远：

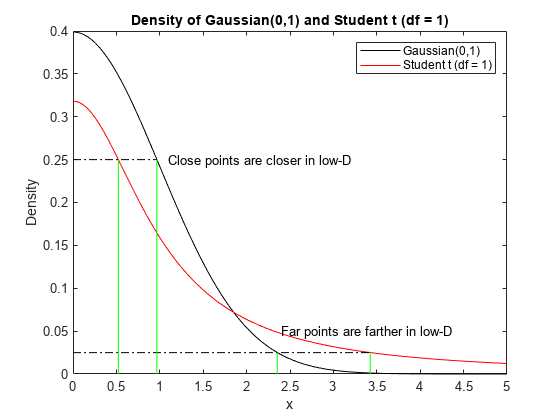
也就是说，原来 x-space 上的点如果存在一些 gap（similarity 较小），这些 gap 就会在映射到 z-space 后被强化，变的更大更大。

Unsupervised Learning: Neighbor Embedding

著名的 tSNE 算法（'NE' --- Neighbor Embedding）

manifold Learning

manifold 与 欧氏距离失效

什么是 manifold，manifold 其实就是一个 2D 平面被卷曲起来成为一个3D物体，其最大的特点是3D空间中的两点之间Euclidean distance并不能衡量两者在(卷曲前)2D空间中的'远近'，尤其是两者距离较大的时候，欧式几何不再适用 --- 3D远距离情况下欧式几何失效问题，在3D空间中欧式几何只能用在距离较近的时候。

manifold learning 就是针对3D下欧式几何失效问题要做的事情就是把卷曲的平面摊平，这样可以重新使用欧式几何求解问题(毕竟我们的很多算法都是基于 Euclidean distance)。这种摊平的过程也是一种降维过程。

manifold learning algo-1: LLE

又是一种“你的圈子决定你是谁”的算法

第一步, 计算 w

针对每个数据集中的点，【选取】他的K（超参数，类似KNN中的K）个邻居，定义名词该\(x^i\)点与其邻居\(x^j\)之间的【关系】为：\(w_{ij}\), \(w_{ij}\) represents the relation between \(x^i\) and \(x^j\)

\(w_{ij}\) 就是我们要寻找的目标，我们希望借由 \(w_{ij}\) 使得 \(x^i\) 可以被K个邻居通过\(w_{ij}\)的加权和来近似，使用 Euclidean distance 衡量近似程度:

given \(x_i, x_j\),, find a set of \(w_{ij}\) minimizing

\(w_{ij} = argmin_{w_{ij},i\in [1,N],j\in [1,K]}\sum_i||x^i - \sum_jw_{ij}x^j||_2\)

第二步, 计算 z 做降维，keep \(w_{ij}\) unchanged, 找到 \(z_{i}\) and \(z_{j}\)将 \(x^i, x^j\) 降维成\(z^i, z^j\), 原则是保持 \(w_{ij}\) 不变，因为我们要做的是 dimension reduction, 所以新产生的 \(z_i, z_j\) 应该比 \(x_i, x_j\) 的维度要低：

given \(w_{ij}\), find a set of \(z_i\) minimizing

\(z_{i} = argmin_{z_{i},i\in [1,N],j\in [1,K]}\sum_i||z^i - \sum_jw_{ij}z^j||_2\)

LLE 的特点是：它属于 transductive learning 类似 KNN 是没有一个具体的函数（例如: \(f(x)=z\)）用来做降维的.

LLE 的一个好处是：看算法【第二步】，及时我们不知道 \(x_i\) 是什么，但只要知道点和点之间的关系【\(w_{ij}\)】我们依然可以使用 LLE 来找到 \(z_i\) 因为 \(x_i\) 起到的作用仅仅是找到 \(w_{ij}\)

LLE 的累赘：必须对 K（邻居数量）谨慎选择，必须刚刚好才能得到较好的结果。

• K 太小，整体 w （模型参数）的个数较少，能力不足，结果不好

• K 太大，离 \(x_i\) 较远距离的点（x-space 就是卷曲的 2D 平面）也被考虑到，之前分析过 manifold 的特点就是距离太大的点 Euclidean distance 失效问题。而我们的公式计算 w 的时候使用的就是 Euclidean distance，所以效果也不好。

这也就是为什么 K 在 LLE 中非常关键的原因。

manifold learning algo-1: Laplacian Eigenmaps

Graph-based approach, to solve manifold

算数据集中点的两两之间的相似度，如果超过某个阈值就连接起来，如此构造一个 graph。得到 graph 之后，【两点之间的距离】就可以被【连线的长度】替代，换言之 laplacian eigenmaps 并不是计算两点之间的直线距离（euclidean distance）而是计算两点之间的曲线距离:

回忆我们之前学习的 semi-supervised learning 中关于 graph-based 方法的描述：如果 x1 和 x2 在一个 high-density region 中相近，那么两者的标签（分类）相同，我们使用的公式是：

\(L=\sum_{x^r}C(y^r, \hat{y}^r)\) + \lambda S

\(S=\frac{1}{2}\sum_{i,j}w_{i,j}(y^i - y^j)^2=y^TLy\)

\(L = D - W\)

\(w_{i,j} = similarity between i and j if connected, else 0\)

• \(x^r\)： 带标数据
• \(S\)： 图(从整个数据集绘出)的平滑度
• \(w\)：两点之间的相似度，也就是graph的边的值
• \(y^i\)：预测标签
• \(\hat{y}^r\)：真实标签
• \(L\)： graph 的 laplacian

同样的方法可以用在 unsupervised learning 中, 如果 xi 与 xj 的 similarity(\(w_{i,j}\)) 值很大，降维之后（曲面摊平之后）zi 和 zj 的距离(euclidean distance)就很近:

\(S=\frac{1}{2}\sum_{i,j}w_{i,j}(z^i - z^j)^2\)

但是仅仅最小化这个 S 会导致他的最小值就是 0，所以要给 z 一些限制 --- 虽然我们是把高维的扭曲平面进行摊平，但我们不希望摊平（降维）之后他仍然可以继续'摊'(曲面 ->摊平,依然是曲面 -> 继续摊), 也就是说我们这次摊平的结果应该是【最平的】，也就是说：

if the dim of z is M, \(Span{z^1, z^2, ..., z^N} = R^M\)

【给出结论】可以证明的是，这个 z 是 Laplacian (\(L\)) 的比较小的 eigenvalues 的 eigenvectors。所以整个算法才叫做 Laplacian eigenmaps, 因为他找到的 z 就是 laplacian matrix 的最小 eigenvalue 的 eigenvector.

Spectral clustering: clustering on z

结合刚才的 laplacian eigenmaps, 如果对 laplacian eigenmaps 找出的 z 做 clustering(eg, K-means) 这个算法就是 spectral clustering.

spectral clustering = laplacian eigenmaps reduction + clustering

T-distributed Stochastic Neighbor Embedding(t-SNE)