Dimension Reduction 为什么可能是有用的?
一,例子1
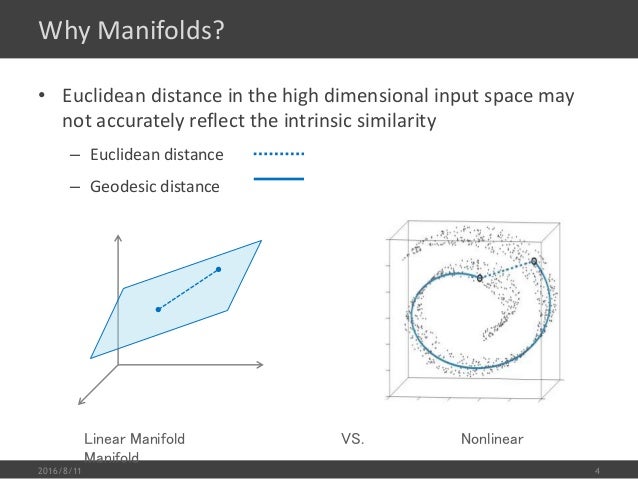
为什么 Dimension Reduction 可能是有用的,如下图示:

如果我们用 3 dimension 的样本维度去描述他其实是非常浪费的,因为很明显他是卷曲在一起的,如果我们有办法把他展平,不同类型(不同颜色代表不同类型)就很容易区隔开,而展平之后我们只需要 2 dimension 的样本维度。所以根本不需要把这个问题放在 3d 中去考虑,2d 就可以了。

二,例子2
在手写数字辨识的任务中,你或许根本用不到 28*28 的维度,比如数字 3 他可能有很多形态,但其实大部分都是旋转一下角度而已,所以对于辨识 3 这件事可能需要的维度仅仅是一个旋转角度而已(1维度)
如何做 dimension reduction 呢?
对数据降维就是找一个function
\(f(x) \rightarrow x', dim(x) >> dim(x')\)
一,方法1: feature selection (略)
二,方法2:PCA
基本原理
PCA 的本质就是通过一个一次线性函数 \(W^Tx\)把高维度的数据样本转换为低维度的数据样本。就像 \(w^Tx\) 如果\(W^T\)矩阵只有一行,这个函数就是两个向量的内积 --- 结果是一个(一维)数值,如果 \(W^T\) 是一个矩阵,那么 \(W^T\) 有多少行最终内积结果就有多少维:
$$
R_W^{1*N} \cdot R_x^{N*1} = R_{x'}^{1*1}
R_W^{2*N} \cdot R_x^{N*1} = R_{x'}^{2*1}
...
$$
\(f(x) \rightarrow x', dim(x) >> dim(x')\)
\(z = Wx, to\ find\ 'W'\)
找到优化问题 --- projection has max variance
该如何找到 W 呢,从最简单的开始,我们假设 :
- reduce x to 1 D vector z, means that 'z' is a digit
- 'W' matrix only have ONE row
- this row's L2 norm is equal to 1: \(||w^1||_2=1\).
如此一来,'z' 就可以看做是 'x' 在 'w' 方向上的投影(内积的几何意义)。
所有的 x: \(x^1, x^2, x^3,...\) 都在 w 方向上做投影就得到了 z: \(z^1, z^2, z^3,...\) , 而我们要做的就是从:
如何找到 W 变成 找到一个 x 的更好的投影方向
we want the variance of \(z_1\) as large as possible.
variance 在图像上的表现就是,投影之后的 z 的取值范围(值域),取值范围越大variance越大。
对于投影到一维空间,找到最佳的 w('w' is a row vector) 使得 x('x' is N dimension) 投影到该方向得到的 z ('z' is a digit)的 variance 是最大的, 用公式表示就是:
\(find\ a\ w\ to\ maximize:\)
\(Var(z_1) = \sum_{z_1}(z_1 - \bar{z_1})^2)\)
\(with\ constaint\ :\ ||w_1||_2=1\)
对于投影到二维(甚至多维)空间,我们要给每个后面的w一个限制就是: 后面的 w(n+1 th row) 要跟前面的所有 w({1~n} rows) 相互垂直, \(w_{n+1} \cdot \{w_{i}\}_{i=1}^n = 0\).
整体来看就是:
the 1st row of W should be:
\(w_1 = argmax(Var(z_1) = \sum_{z_1}(z_1 - \bar{z_1})^2)\)
\(constraint:\ ||w_1||_2=1\)
the 2nd row of W should be:
\(w_2 = argmax(Var(z_2) = \sum_{z_2}(z_2 - \bar{z_2})^2)\)
\(constraint:\ ||w_2||_2=1, w_2 \cdot w_1 = 0\)
the 3rd row of W should be:
\(w_3 = argmax(Var(z_3) = \sum_{z_3}(z_3 - \bar{z_3})^2)\)
\(constraint:\ ||w_3||_2=1, w_3 \cdot w_1 = 0, w_3 \cdot w_2 = 0\)
.......
then the W should be:
$$
W = \begin{vmatrix} (w_1)T \\ (w_2)T \\ . \\ . \\ . \end{vmatrix}\quad
$$
这里 W 会是一个 Orthogonal matrix, 因为每一行的 norm 都等于1,并且行行之间相互垂直。
求解这个带限制条件优化问题 ---- 拉格朗日乘数法
Lagrange multiplier 可以把带限制条件的优化问题转换>为无限制优化问题: target - a(zero_form of >constraint1) - b(zero_form of constraint2)
无限制的优化问题,就可以通过偏微分=0来找到最优解
如果 W 矩阵只有一行
$$
one\ x\ one\ z_1
\bar{z_1} = \sum{z_1} = \sum{w_1 \cdot x} = w_1 \cdot \sum x = w_1 \cdot \bar{x}
Var(z_1) = \sum_{z_1}(z_1 - \bar{z_1})^2
= \sum_x(w_1 \cdot x - w_1 \cdot \bar{x})^2
= \sum_x(w_1 \cdot (x-\bar{x}))^2
$$
对于 \(w \cdot (x - \bar{x})\), 他是两个向量的内积,对于这种内积的平方,要注意如下的惯用转换公式(值得记住)。
$$
(a \cdot b)^2 = (a^Tb)^2
$$
因为 \(a \cdot b\) 是内积,是一个数值,数值的平方无关乎顺序,所以可以写成:
$$
(a^Tb)^2 = a^Tba^Tb
$$
因为 \(a \cdot b\) 是内积,是一个数值,数值的转置还是自身,所以可以写成:
$$
(a^Tba^Tb = a^Tb(a^Tb)^T
$$
化简之后:
$$
a^Tb(a^Tb)^T = a^Tbb^Ta
$$
所以之前 var 的式子可以化简为:
$$
Var(z_1) = \sum_{z_1}(z_1 - \bar{z_1})^2
= \sum_x(w_1 \cdot x - w_1 \cdot \bar{x})^2
= \sum_x(w_1 \cdot (x-\bar{x}))^2
= \sum_x(w_1)^T(x-\bar{x})(x-\bar{x})^Tw_1
$$
因为是对 x 来求和,所以 w 可以提出去:
$$
Var(z_1) = \sum_{z_1}(z_1 - \bar{z_1})^2
= \sum_x(w_1 \cdot x - w_1 \cdot \bar{x})^2
= \sum_x(w_1 \cdot (x-\bar{x}))^2
= \sum_x(w_1)^T(x-\bar{x})(x-\bar{x})^Tw_1
= (w_1)^T(\sum_x(x-\bar{x})(x-\bar{x})^T)w_1
$$
其中 \(\sum_x(x-\bar{x})(x-\bar{x})^T\) 是什么,这个是 x 向量(样本都是向量)的 covariance matrix. covariance 是对称且半正定对的, 也就是说所有的 eigenvalues 都是非负的
$$
Var(z_1) = \sum_{z_1}(z_1 - \bar{z_1})^2
= \sum_x(w_1 \cdot x - w_1 \cdot \bar{x})^2
= \sum_x(w_1 \cdot (x-\bar{x}))^2
= \sum_x(w_1)^T(x-\bar{x})(x-\bar{x})^Tw_1
= (w_1)^T(\sum_x(x-\bar{x})(x-\bar{x})^T)w_1
= (w_1)^TCov(x)w_1
$$
我们设 \(S = Cov(x)\) ,于是我们得到了一个新的优化问题:
find w1 maximizing:
\(w_1^T S w_1, with\ constraint\ ||w_1||_2 = 1, means\ w_1^Tw_1 = 1\)
Lagrange multiplier is target - zero_form of constraints
之前说明过 \(w_1\) 是 W 矩阵的第一个row,再次提醒下。
\(g(w_1) =w_1^TSw_1 - \alpha(w_1^Tw_1 - 1)\)
\(\frac{\partial g(w_1)}{\partial w_{11}} = 0\)
\(\frac{\partial g(w_1)}{\partial w_{12}} = 0\)
....
通过对 Lagrange 式子 \(g(w_1)\) 的微分为0来求最大最优的w,可以得到如下化简后的式子:
\(Sw_1 - \alpha w_1 = 0\)
\(Sw_1 = \alpha w_1\)
这种形式我们就熟悉了,\(w_1\) 是 S 的 eigen vector
但是这样的 w1 有很多,因为 S 的 eigen vector 有很多,所以 w1 的潜在选择也很多,哪一个是最好的选择呢?通过我们的优化目标来判断。
\(w_1^TSw_1 = \alpha w_1^Tw_1 = \alpha\)
而这里的 \(\alpha\) 是 eigen value,
所以,因为我们要最大化的目标最后等于 alpha, 而 alpha 是 eigen value, 所以我们选择最大的 eigen value, 一个 eigen value 对应一个 eigen vector, 所以最优的 w1 就是最大的 eigen value 对应的那个 eigen vector.
之前分析过, Find w2 的情况与 Find w1 略有不同,不同在优化问题的限制条件多出一个与之前所有的w都垂直,那么就是:
\(Find\ w_2\ maximizing: w_2^TSw_2, w_2Tw_2=1, w_2^Tw_1=0\)
按照 目标函数 - 系数*zero_form of 限制条件 的拉格朗日使用方法,可以得到如下无限制条件的优化问题:
如果 W 矩阵有多行
对于 W 矩阵有多行的情况,优化目标函数需要改变, 要增加限制条件,如果不加改变的话你得到的 wn 永远与 w1 一样,增加的这个限制条件是:后面的每个w都要与前面的所有w相互垂直 --- 内积为0。
\(Find\ w_2\ maximizing:\)
$$
g(w_2) = w_2^TSw_2 - \alpha(w_2^Tw_2-1)-\beta(w_2^Tw_1-0)
$$
同样的通过微分等于0来求无限制条件的优化问题:
\(\frac{\partial g(w_1)}{\partial w_{11}} = 0\)
\(\frac{\partial g(w_1)}{\partial w_{12}} = 0\)
化简上述结果可以得到:
\(Sw_2 - \alpha w_2 - \beta w_1 = 0\)
上述等式两边同时乘以 w1:
\(w_1^TSw_2 - \alpha w_1^Tw_2 - \beta w_1^Tw_1 = 0\)
\(w_1^TSw_2 - \alpha * 0 - \beta * 1 = 0\)
因为 \(w_1^TSw_2\) 本身是一个 向量矩阵向量 的形式,他是一个数值,数值的转置还是自身:
\(w_1^TSw_2 = (w_1STw_2)^T = w_2^TS^Tw_1\)
因为 S 是 Covariance Matrix of x, 是对称的,所以 \(S^T=S\)
\(w_2^TS^Tw_1= w_2^TSw_1\)
使用 w1 的结论,\(Sw_1 = \lambda_1w_1\), 所以有
\(w_2^TSw_1=\lambda_1w_2^Tw_1=0\)
所以,综合起来看:
\(w_1^TSw_2 - \alpha w_1^Tw_2 - \beta w_1^Tw_1 = 0\)
\(w_1^TSw_2 - \alpha * 0 - \beta * 1 = 0\)
\(0 - \alpha * 0 - \beta * 1 = 0\)
所以:
\(\beta=0\)
所以:
\(Sw_2 - \alpha w_2= 0\)
\(Sw_2 = \alpha w_2\)
由于 w2 也是 eigen vector, 同样有很多选择,与 w1 选择的依据一样,我们只能选择剩下最大的那个 eigenvalue of S 对应的 eigenvector
so,结论是:
$$
z = Wx
$$
$$
W = \begin{vmatrix} (w_1)T \\ (w_2)T \\ . \\ . \\ . \end{vmatrix}\quad
$$
$$
W = \begin{vmatrix} 1st\ largest\ eigenvalues'\ eigenvector\ of\ Cov(x) \\ 2nd\ largest\ eigenvalues'\ eigenvector\ of\ Cov(x) \\ 3rd\ largest\ eigenvalues'\ eigenvector\ of\ Cov(x) \\ ...\end{vmatrix}
$$
PCA 的副产品 --- 降维后数据点的各个维度互相垂直
数据点的各个维度互相垂直
用数学语言来表述就是
数据点的协方差矩阵是一个 Diagonal matrix
也就是
数据点的各个维度之间没有 correlation
这样有什么作用呢?
一个很好的作用是,原来的 data 经过 PCA 之后输出的新的 data 可以接其他较为简单的(或是对数据点维度要求无 correlation 的)model ---> eg. Naive Bayes.
如何证明呢?
$$
Cov(z) = \sum(z - \bar{z})(z-\bar{z})^T
$$
这一项,可以可以展开合并后成为下面这种形式:
$$
Cov(z) = \sum(z - \bar{z})(z-\bar{z})^T = WSW^T,\ \ S = Cov(x)
$$
$$
W^T=\begin{vmatrix} w_1 \\ .\\.\\.\\ w_k \end{vmatrix}^T= [w_1, ..., w_k]
$$
注意转置之前 w1 是 W矩阵的行向量,转置后,w1 是 W^T 的 列向量:
$$
\begin{vmatrix}
1 & 2 & 3 & \rightarrow w_1\\ 4 & 5 & 6 & \rightarrow w_2 \\ 7 & 8 & 9 & \rightarrow w_3
\end{vmatrix}^T
\rightarrow
\begin{vmatrix}
1 & 4 & 7 \\ 2 & 5 & 8 \\ 3 & 6 & 9 \\ \downarrow & \downarrow & \downarrow \\ w_1 & w_2 & w_3
\end{vmatrix}
$$
$$
WSW^T = WS[w_1, ..., w_k] = W[Sw_1, ..., Sw_k]
$$
利用之前的结论:
\(Sw_1 = \lambda_1 w_1\)
$$
W[Sw_1, ..., Sw_k] = W[\lambda_1 w_1, ..., \lambda_k w_k] = [\lambda_1Ww_1, ..., \lmabda_kWw_k] = [\lambda_1e_1, ..., \lambda_ke_k]
$$
其中 \(e_i\) 是指第 \(i\) 位为 1, 其余位都为 0 的列向量。
所以 \(Cov(z)\) 就是一个 Diagonal matrix.
总结
PCA 关键词:
- linear function, projection
- maximize Variance of z
- Covariance Matrix of x
- eigenvector of Covariance Matrix
一个重要的结论需要记住:
Covariance Matrix is a symmetric, positive-semidefinite matrix, so it has non-negative eigenvalues
一个重要的技术:
带限制条件优化
--- Lagrange multiplier --->
无限制条件优化
--- partial dirivitive = 0 --->
求解。
一个重要的机器学习常识:
数据点的各个维度互相垂直
用数学语言来表述就是
数据点的协方差矩阵是一个 Diagonal matrix
也就是
数据点的各个维度之间没有 correlation