Analogies exist between rotational and translational physical quantities. Identify the rotational term analogous to each of the following: acceleration, force, mass, work, translational kinetic energy, linear momentum, impulse.
Would make a good matching set. : )
2: (a) Calculate the magnitude of the acceleration due to gravity on the surface of Earth due to the Moon. (b) Calculate the magnitude of the acceleration due to gravity at Earth due to the Sun. (c) Take the ratio of the Moon’s acceleration to the Sun’s and comment on why the tides are predominantly due to the Moon in spite of this number.
A nice study workout, similar to HW 07.
to show that the motion of heavenly bodies should be conic sections
Kepler's first law of planetary motion, before Newton, had discovered this conic section idea, but Newton SHOWED or PROVED as in geometric analysis that conic sections were required, no coincidence.
Recall that the acceleration due to gravity is about on Earth.
We reviewed a bunch of this section in the Geospatial energy levels mini-lecture in YouTube.
an equation for
Excellent.
3: Draw a free body diagram for a satellite
nice study task
both
terrestrial and celestial, which at the time of Newton, were not universally considered as a unified system with universal laws governing both realms. In fact, the verification of Newton's law of universal gravitation simplified our view of the physical universe: one book to describe them all, as Galileo foretold.
some systems in stable equilibrium are more stable than others.
A system is in unstable equilibrium if, when displaced, it experiences a net force or torque in the same direction as the displacement from equilibrium
Two children of mass 20.0 kg and 30.0 kg sit balanced on a seesaw with the pivot point located at the center of the seesaw. If the children are separated by a distance of 3.00 m, at what distance from the pivot point is the small child sitting in order to maintain the balance?
Basic calculation
For earthquakes, there are several types of disturbances, including disturbance of Earth’s surface and pressure disturbances under the surface.
Another seismic wave phenomenon is a seiche
Cf., What is a seiche?
For earthquakes, there are several types of disturbances, including disturbance of Earth’s surface and pressure disturbances under the surface.
Sound waves in air and water are longitudinal.
and energy
Also momentum. Because electromagnetic radiation propagates momentum and energy across spacetime, we have an opportunity to harness sunlight in outer space and use it in a solar sail, to navigate here and there in the solar system.
Sound in solids can be both longitudinal and transverse.
E.g., the s and p waves from earthquakes, although the liquid outer core of Earth does not permit s waves to propagate, because s waves are transverse.
In equation form
Generic wave equation. For electromagnetic radiation, the wave equation is \(c=\lambda f\), where the speed of light \(c=3\times 10^8 \frac{m}{s}\).
Calculate the moment of inertia of a skater given the following information. (a) The 60.0-kg skater is approximated as a cylinder that has a 0.110-m radius. (b) The skater with arms extended is approximately a cylinder that is 52.5 kg, has a 0.110-m radius, and has two 0.900-m-long arms which are 3.75 kg each and extend straight out from the cylinder like rods rotated about their ends.
This would not be a brain burner, to make you think, but a rotational torture device. I will not put ANYTHING like this on Exam 3.
Starting with the formula for the moment of inertia of a rod rotated around an axis through one end perpendicular to its length prove that the moment of inertia of a rod rotated about an axis through its center perpendicular to its length is You will find the graphics in Figure 3 useful in visualizing these rotations.
This would be easy to figure out as a lecture exercise, but not on Exam 3.
MAKING CONNECTIONS
Extensive discussion about this Figure 3 in Friday's lecture.
Some rotational inertias.
All of these moments of inertia are the result of counting up the quantity \(mr^2\) for each pixel of mass, \(I=\sum_{\text{pixels}} \left(mr^2\right)\) To do this task, you usually need calculus, although the hoop can be done with straight trig, no calc.
Notice that each moment of inertia is a fraction or multiple of total mass \(M\) multiplied by the square or sum of squares of the overall dimension \(R^2\) or \(a^2+b^2\) etc. That is because each object in the table has some symmetry which simplifies the calculus and therefore simplifies the formula.
Example 1: Calculating the Effect of Mass Distribution on a Merry-Go-Round
We will be demonstrating this stuff in lecture, 03/22/19
Instead of memorizing these equations, it is helpful to be able to determine them from reason.
The brake cable on a bicycle carries the tension T from the handlebars to the brake
general result that if friction on an incline is negligible, then the acceleration down the incline is regardless of mass.
Still, do not memorize this.
Yup, previous annotation is verified.
To do this, draw the right triangle
This is why I always say that intro physics is SO filled with right triangles. 
Flexible connectors are often used to transmit forces around corners
adding are perpendicular to each other and thus form a right triangle. This means that we can use the Pythagorean theorem to calculate the magnitude
there are no additional forces on the ball in the horizontal direction
static friction is a responsive force, being able to assume a value less than but no more than
1: (a) A 22.0 kg child is riding a playground merry-go-round that is rotating at 40.0 rev/min. What centripetal force must she exert to stay on if she is 1.25 m from its center?
Basic
What is the ideal banking angle for a gentle turn of 1.20 km radius on a highway with a 105 km/h speed limit (about 65 mi/h), assuming everyone travels at the limit?
Good.
Let us now consider banked curves,
Tire friction enables a vehicle to take the curve at significantly higher speeds.
In cases in which forces are not parallel, it is most convenient to consider components along perpendicular axes—in this case, the vertical and horizontal directions.
Similar to the Bumblebee tilt test.
much, much less than the speed of light
his ideas were eventually accepted by the church and scientific communities.
A short paragraph to describe a very complex controversy! The paragraph is acceptable, but does not do it justice. Well worth reading about, e.g., Galileo's Daughter, by Dava Sobel (UCF Main Library General Collection - 4th Floor QB36.G2 S65 1999 Available)
Non-relativistic, v << c.
Kinematics of Rotational Motion
Not a total bypass but we did not talk too much about this information in lecture.
four rotational kinematic equations (presented together with their translational counterparts):
nice
the force (to bring the occupant to a stop) will be much less if it acts over a larger time.
Perfect description
average effective force
equivalent effective force
Idealized force structure
When opening a door, you push on it perpendicularly with a force of 55.0 N at a distance of 0.850m from the hinges. What torque are you exerting relative to the hinges?
Basic calculation
The torque is always calculated with reference to some chosen pivot point. For the same applied force, a different choice for the location of the pivot will give you a different value for the torque, since both and depend on the location of the pivot. Any point in any object can be chosen to calculate the torque about that point. The object may not actually pivot about the chosen “pivot point.”
This is important later when we consider angular momentum in an astronomical setting, where the axis of rotation is not necessarily the center of the orbit. In fact, an astronomical object like 'Oumuamua might not even be on a bound orbit, but an unbound orbit -- it enters the solar system, interacts gravitationally with the Sun and then exits the solar system. 
Torque plays the same role in rotational motion that force plays in linear motion.
Example 2: Calculating Force: Venus Williams’ Racquet
Good.
when the mass of the system is constant
Compare the player’s momentum with the momentum of a hard-thrown 0.410-kg football
Poor comparison. A better comparison is with another player of similar though different mass and with velocity \(v=8.00 \frac{m}{s}\) and antiparallel to the first player's velocity.
The net external force equals the change in momentum
$$F_{net}=ma$$
$$F_{net}=m \frac{\Delta v}{\Delta t}$$
$$F_{net}=\frac{m \Delta v}{\Delta t}$$
and for objects with constant mass, $$m \Delta v = \Delta \left(mv\right)$$ so $$F_{net}=\frac{\Delta p}{\Delta t}$$
An object that has a small mass and an object that has a large mass have the same momentum. Which object has the largest kinetic energy? 2: An object that has a small mass and an object that has a large mass have the same kinetic energy. Which mass has the largest momentum?
Two good study questions.
The angles that vectors and make
The angles here are not that helpful. Main thing is to build resultant from four components Ax, Ay, Bx, By, then get the trig on the resultant R
Figure 6. To add vectors A and B
Lovely diagram
Extrapolating to a frictionless surface
an extrapolation that Galileo first made.
find the masses of heavenly bodies
E.g., black holes like Cygnus X-1 and Sagittarius A*, the enormous black hole \(\approx 4\times 10^6 M_{\odot}\) at the center of the Milky Way galaxy.
a small set of rules and a single underlying force
This is why Halley's successful prediction was so important.
In the next image, her rate of spin increases greatly when she pulls in her arms, decreasing her moment of inertia.
As a student observed, \(I\) and \(\omega\) vary inversely when angular momentum is conserved.
Suppose a child walks from the outer edge of a rotating merry-go round to the inside. Does the angular veloc
Good conceptual question
Calculating the Angular Momentum
It is enough for us to predict "larger \(\omega\)" or "smaller \(\omega\)" etc., and not necessarily calculate L to the nearest \(0.001 \,kg\,m^2\). After Exam 3, we will do some full calculations, however.
can be added using the familiar head-to-tail method or by trigonometric methods.
i.e., graphical or analytical methods
In physics, the definition of time is simple
Oh, no! Nothing could be further from the truth! But we can provisionally accept this statement for the moment.
10.4
Ready to work on this topic starting 03/27
There is no simple, yet accurate, scientific definition for energy.
In fact, energy is a deep mystery, like entropy and time. There is no standard Joule on display inside a glass case in Paris at the famous Rotonde du Assiette de Crevettes or anything like that. Prof. Richard Feynman taught that energy can be calculated in various ways but he was stumped as to what it is.
It is important to realize that in physics today, we have no knowledge of what energy is. ...there are formulas for calculating some numerical quantity, and when we add it all together it [is] always the same number. [Feynman Lectures]
almost
Huh?
Because gravitational potential energy depends on relative position, we need a reference level at which to set the potential energy equal to 0.
Note: in the geospatial mini-lecture, the zero of GPE was at infinity.
9-megaton fusion bomb
ridiculous
Potential Energy of a Spring
Bypass until after Exam 3.
Collisions of Point Masses in Two Dimensions
Bypass until after Exam 3
It can help us make predictions.
HUGE
the force exerted by the person pushing the mower must be greater than the friction opposing the motion
Same as the relationship between the propulsion force Fp from the road surface on the chopper and the friction force f, in the homework
Introduction to Rocket Propulsion
We have talked about rocket motors and their effects, but consider this section is a bypass.
It can be shown that
Biggest lie in physics. "It can be shown that..." is usually the place where the author is thinking about calculus but does not want to actually show it.
restoring force.
most fishermen feel no obligation to truthfully report the mass
Good one. 
Here, is the restoring force, is the displacement from equilibrium or deformation, and is a constant related to the difficulty in deforming the system. The minus sign indicates the restoring force is in the direction opposite to the displacement.
See previous note.
If we follow a small volume of fluid along its path,
Typical strategy for understanding fluid dynamics.
This equation tells us that, in static fluids, pressure increases with depth
We already knew this.
When a fluid flows into a narrower channel, its speed increases.
2: A 75.0-kg person climbs stairs, gaining 2.50 meters in height. Find the work done to accomplish this task.
Reminiscent of the concepts in Written HW 07
How much work is done by the boy pulling his sister 30.0 m in a wagon as shown in Figure 3? Assume no friction acts on the wagon
A good basic work calculation in two dimensions.
2: Give an example of a situation in which there is a force and a displacement, but the force does no work. Explain why it does no work.
Good question. Under what conditions will an applied force do zero work? It is a geometric question, really.
The directions of the velocity of an object at two different points are shown, and the change in velocity Δv is seen to point directly toward the center of curvature. (See small inset.) Because ac = Δv/Δt, the acceleration is also toward the center; ac is called centripetal acceleration. (Because Δθ is very small, the arc length Δs is equal to the chord length Δr for small time differences.)
Similar to my derivation, 2/15
Example 1: How Does the Centripetal Acceleration of a Car Around a Curve Compare with That Due to Gravity?
Good example.
Example 2: How Big Is The Centripetal Acceleration in an Ultracentrifuge?
Another good example.
the resultant is independent of the order in which the vectors are added.
the negative of any vector has the same magnitude but the opposite direction,
The topic of chaos has become quite popular over the last few decades.
Figure 1. (a) A graph
Discussed this in lecture.
rotational kinetic energy
Rotational KE is simple to handle, but we will tackle it after Exam 3.
On the whole, solutions involving energy are generally shorter and easier than those using kinematics and dynamics alone.
This is why scientists work most of quantum mechanics and relativity in terms of energies, not F = ma forces.
This expression
Work and change in kinetic energy, \(W=\Delta \left( KE \right)\)
Example 4: Work and Energy Can Reveal Distance, Too
Stopping distance problem, a classic exercise
momentum, which will affect the outcome of their collisions
Many systems oscillate, and they have certain characteristics in common.
True. And this is why physicists spend so much time thinking about spring/mass systems.<br>
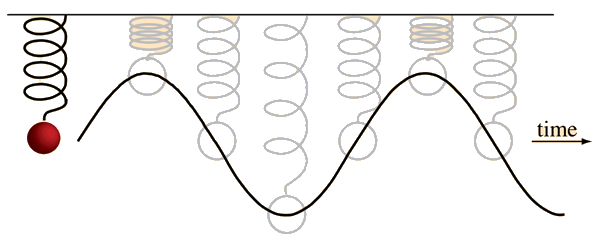That is, what is simple to learn about spring/mass systems becomes widely applicable in other oscillatory systems like a beating heart, a particle inside an atom's nucleus, a light wave, a tsunami etc.
guitar, atoms
Atoms and guitars ← ← you will savvy this analogy in PHY2054C!!
The forces due to pressure have well-defined directions: they are always exerted perpendicular to any surface.
“Aerodynamic” shaping
The National Advisory Committee for Aeronautics (NACA), where Hidden Figures' Katherine Johnson rose, was originated during WW I, was an intensive research facility focused on airframe optimization -- aerodynamic shaping. One famous airframe became the P51 Mustang, a prime fighter against the German Luftwaffe.
Katherine Johnson at NASA Langley 
Suppose you attach the object with mass to a vertical spring originally at rest, and let it bounce up and down. You release the object from rest at the spring’s original rest length. (a) Show that the spring exerts an upward force of on the object at its lowest point. (b) If the spring has a force constant of and a 0.25-kg-mass object is set in motion as described, find the amplitude of the oscillations. (c) Find the maximum velocity.
air resistance is negligible
Simple Machines
Bypass, although it is an interesting section to read if you are interested.
Let's try this homework assignment: Experimental assignment.
$$c = \lambda f$$
Models for an Expanding Universe
Bypass My balloon analogy in Mini-Lecture C is better.
Variation of Hubble’s Constant
Bypass
Hubble’s Law
Bypass
f we then put this speed and the Hubble constant into Hubble’s law equation, we can solve for the distance.
Or, more simply, read it off the diagram.
Basically, if we can obtain a spectrum of a galaxy, we can immediately tell how far away it is.
Yes, definitely handy, because if we make a big telescope we can see and catch spectra of really distant, faint galaxies!
E.g., from Kirshner, PNAS, 2004,
just as Lemaître had suggested.
Lemaître was correct!!!! It forced Einstein to say that his own model of all galaxies was the biggest scientific mistake of his life.
When Hubble laid his own distance estimates next to measurements of the recession velocities (the speed with which the galaxies were moving away), he found something stunning: there was a relationship between distance and velocity for galaxies. The more distant the galaxy, the faster it was receding from us.
There is a legend about this, that this relation came to Hubble as he drove down to Pasadena after a night's observing. He pulled his car over on the shoulder and stopped to think. It is a twisty mountain road; I have driven it myself. At some time later, hours later as the legend goes, a traffic cop pulled alongside to check him out. All was well -- he was just thinking of what it all meant, that the entire universe was expanding. Edwin Hubble was probably very late for his breakfast, and we still ponder this meaning today.
Humason was collaborating with Hubble by photographing the spectra of faint galaxies
They were especially looking at the near-ultraviolet H and K lines of calcium, $$\lambda_H=396.8\:nm\longrightarrow\text{toward red, longer wavelengths}$$
$$\lambda_K=393.4\:nm\longrightarrow\text{also toward red, longer wavelengths}$$
Here is an image of the sun in a filter that only transmits the Ca K line, very purply blue.
So a galaxy's K line will be less purply blue, maybe an aqua blue or even green... i.e., shifted toward the red end of the Roy G. Biv spectrum
No one at the time quite knew what to make of this discovery.
Hubble figured it out.
the spectral lines of most galaxies showed an astounding redshift.
BINGO! An unexpected result.
spectra of galaxies contained a wealth of information about the composition of the galaxy and the velocities of these great star systems.
How it was discovered
Other Measuring Techniques
Bypass this. We will concentrate on Cepheid variables and Type Ia supernovas
(credit: NASA, ESA, A. Riess (STScI))
I cannot find the original image on NASA servers. However, this image from 2014 is helpful for visualizing a Type Ia supernova:
Image: Katzman Automated Imaging Telescope/LOSS
"Type Ia supernovae have acquired global importance in recent years through their use as distance indicators..."
Observations show that supernovae of this type all reach nearly the same luminosity (about 4.5 × 109LSun) at maximum light.
So we have to be very alert to catch the peak intensity, "maximum light," before it starts to dim out.
make out an individual cepheid variable star in the galaxy M100 and measure its distance to be 56 million light-years.
Nice!
they could measure distances using certain kinds of intrinsically luminous variable stars, such as cepheids
Handy cepheid variable stars!
we know the precise way light is dimmed by distance
If we know the distance to a galaxy, we can convert how bright the galaxy appears to us in the sky into its true luminosity
For stars and galaxies, apparent luminosity (what we see on Earth) depends on its distance and its intrinsic luminosity (as measured at the galaxy or star itself).
The Formation of the Galaxy
Pretty technical -- we will bypass this section, too.
Stellar Populations
Interesting but we will bypass this section.
First, an asteroid might have ventured too close to the black hole and been heated to a very high temperature
Nifty. This is like seeing a mega-Chelyabinsk event crush into the black hole... seeing it from halfway across the galaxy.
One of the stars has been observed for its full orbit of 15.6 years.
S2
These stars have now been observed for almost two decades,
First one with a good orbital track was S2, on a 15.2 year orbit about the black hole Sgr A*. 
Cf., Schödel R. et al., "A star in a 15.2-year orbit around the supermassive black hole at the centre of the Milky Way" Nature 419, 694–696 (2002),
There are also thousands of stars within a parsec of Sagittarius A*.
There are only a few stars within a parsec of our solar system.
temperature of 10 million K.
Very hot. How was it heated to this temperature?
Very Large Array (VLA) of radio telescopes in Socorro, New Mexico.
supernova remnants
SNR
supermassive black holes by astronomers, to indicate that the mass they contain is far greater than that of the typical black hole created by the death of a single star.
Definition of supermassive black hole. Some galaxies' central black hole is even larger than ours.
less than the diameter of Mercury’s orbit.
It works out to about \(R=46 \,LS\), which would be well inside Mercury's orbit, \(0.39\, AU=193\, LS\)
the mass closer to us can bend the light from farther away. With just the right alignment, the image of the more distant object also becomes significantly brighter.
Gravitational lensing
these should produce dark features in the ultraviolet spectra of objects lying beyond the Galaxy,
Like the absorption features of the Sun, 
various colors picked out by the upper layers of the chromosphere and very hot atmosphere of the sun.
least 2 × 1012MSun, which is about twenty times greater than the amount of luminous matter.
TWENTY TIMES!!!! Holy Toledo! Visible matter is like a drip from a Slurpee!
forced to the reluctant conclusion that this matter is invisible
Astronomers were reluctant to accept this, but it is now undeniable.
Rotation Curve of the Galaxy
There is a ton of fancy calculus behind the blue part of the graph. So the theory literally falls short of observations (red)
indicating a great deal of mass beyond the Sun’s orbit.
...the sign of "dark matter"
heir orbital velocities are even greater than the Sun’s
This would be like Neptune orbiting faster than Earth!!!
should
Yeah, what they SHOULD do.... ain't necessarily so.
objects orbiting at large distances from a massive object will move more slowly than objects that are closer to that central mass.
E.g., a comet really moving fast at perihelion and slowing down at aphelion. E.g., Uranus and Neptune. Nearly the same mass, but orbital semimajor axes 19.2 AU for Uranus and 30 AU for Neptune; their orbital "years" are 84 years for Uranus but 164 years for Neptune.
In science, what seems to be a reasonable assumption can later turn out to be wrong
Scientists must always be humble about their findings
100 billion times the mass of the Sun
$$M_{\text{Milky Way}}=1\times 10^{11}\,M_{\odot}$$
concentrated at a point in the center of the sphere
As in this diagram of a galactic year:
the Galaxy is roughly spherical
Physicists are always making assumptions like this, spherical galaxy, spherical planet, spherical this, spherical that. There is even a nerdish physics joke for which the punch line is, "Consider a spherical cow."
Physics humor. :\
Anyway, physicists do this to make things easier at the start, then they make more detailed, intricate models, as things progress
Kepler Helps Weigh the Galaxy
As previously stated, Kepler's Third Law is EVERYWHERE!!!!
: )
rotation curve
Galactic rotation curves fail, which is the sign of dark matter.
The concentration of matter in the arms exerts sufficient gravitational force to keep the arms together over long periods of time
Big result, very tough to calculate.
Scientists have used supercomputer calculations to model the formation and evolution of the arms.
As mentioned in the previous annotation
might
A big maybe. Scientists make large models with pixels representing stars of various masses and a gravitational interaction, then let the pixels evolve on the computer. This figure is a rough view of such simulations. A good simulation can be helpful, but they are very tough to make.
21-cm line that comes from cool hydrogen
Wavelength \(\lambda = 21\, cm\) is a radio wavelength outside the FM band and the AM band.
Once the light pollution subsides to negligible levels, the Milky Way can be readily spotted arching over the sky on clear, moonless nights.
E.g., Clearwater Lake Recreation Area, up in Ocala National Forest, about 31 miles northwest of UCF.
our Glaxy is not unique in its characteristics. There are many other flat, spiral-shaped islands of stars, gas, and dust in the universe.
Helpful for comparisons.
Heavier-element abundance
Because of the spectral lines of heavier elements like calcium,
We know that this extensive dark matter halo exists because of its effects on the orbits of distant star clusters and other dwarf galaxies that are associated with the Galaxy.
In other words, they are orbiting faster than they would if only the visible stars were present. The visible stars do not have enough mass to control these visible star clusters.
shaped rather like a peanut
OH MY GOODNESS!!!!!!!
Mount Wilson Observatory,
In the mountains above Los Angeles. Unfortunately, LA is too smoggy now and Mount Wilson is not such a hot observatory these days.
In 1785
Just after the Revolutionary War, before the Constitution!
band standing in formation during halftime at a football game
E.g., 
William Herschel was a German musician who emigrated to England and took up astronomy in his spare time.
Musician and astronomer. NICE!
You could do a much better job from a helicopter flying over the city than you could if you were standing in Times Square.
A good analogy.
The variable v is counted as positive if the velocity is one of recession, and negative if it is one of approach. Solving this equation for the velocity, we find
We will tackle this kind of calculation in Module 3 when we study galaxies.
fossil life on Mars
Cf., the famous Martian meteorite, ALH-84001.
no life was detected on Mars.
But the Viking landers still gave us a lot of good data on Mars.
Climate Change on Mars
skip
The rovers (Spirit, Opportunity, and Curiosity)
Small but mighty, the good and faithful rovers that have sent us so much data about Mars.
Some local source of heating must have released this water
Mysterious. Scientists definitely want to figure this out, if we are ever to colonize Mars
The channel is about 2.5 kilometers across.
Compared to the Amazon River, this is shrimpy. The widest point of the Amazon is about 64 km.
They are about the same to the nearest power of 10.
This is a horrible sentence.
When a scientist deals with huge numbers, as in astronomy, it is sometimes "close enough" if they have the same power of 10 in scientific notation.
So a better sentence would be this: \(\text{\color{blue}The mass of frozen water in the Mars polar cap }\)\(\text{\color{blue}is of the same order as the Greenland ice cap}.\)
One commonly hears egghead scientists saying that two quantities "are about the same order," and by that they mean the two quantities are righteous and equivalent.
polar cap area
Using \(\pi r^2\) for the area here is an underestimation, because \(\pi r^2\) is good for a flat circle, but the polar cap is not flat! It is curvature.
However, using \(\pi r^2\) is
together with a great deal of water ice.
We know this by looking for and measuring the infrared spectra of both \(H_2 O\) and \(CO_2\)
Several types of clouds can form in the martian atmosphere.
We would consider the dust clouds of Mars or of Earth (like in the Sahara) as different from the \(H_2 O\) clouds, which are microdroplets of liquid water held aloft by rising air currents.
At a pressure of less than 0.006 bar, the boiling point is as low or lower than the freezing point, and water changes directly from solid to vapor without an intermediate liquid state (as does “dry ice,” carbon dioxide, on Earth).
Sublimation. Good comparison to what \(CO_2\) ice does here at the surface of Earth.
0.007 bar, less than 1% that of Earth.
Standard 1.00 atmosphere of pressure on Earth = 1.01325 bars, or, as they say on the Weather Channel, 1013.25 millibars. This is the atmospheric pressure on a day of fair weather at sea level. A similar fair day in Denver, one mile altitude, would be less than 1013.25 millibars.
Mars atmospheric pressure is 0.007 bar or 7 millibars.
For comparison: The central pressure of a hurricane is considered extremely dangerous if it gets to 900 millibars. E.g., Hurricane Irma hit the Florida Keys in 2017 at Category 4, 929 millibars central pressure. Very violent.
We know that the one requirement shared by all life on Earth is liquid water.
Astronomers' preoccupation with \(H_2 O\)
Mars seems to be the most promising place to look for life
Our pre-occupation with Mars, e.g., The War of the Worlds.
The most remarkable thing about these organic molecules is that they include equal numbers with right-handed and left-handed molecular symmetry.
This is a huge mystery, the handedness of sugars and amino acids.
complex organic molecules in them—chemicals based on carbon, which on Earth are the chemical building blocks of life.
The other kind of molecule that astronomers are always alert for!!
with the different materials sorted according to density.
like what a centrifuge does.
This value (which we round off to 4.5 billion years in this book) is taken to represent the age of the solar system
Isotopes tell us this age!
Some Striking Meteorites
Cool!
do not appear to come from the comets
Comets are an entire other subject!!
Such a fall occurs when a single larger object breaks up during its violent passage through the atmosphere
Excellent example is the Allende meteorite, which fell as a larger object that broke up, down in Mexico, on Feb. 8, 1969.
It is the pattern of lines
I.e., its quantum fingerprints!
Check Your Learning
Another redshift.
656.6 nm
So \(\Delta \lambda = 0.3 nm\) which is in the numerator of the equation below.
difference in wavelength
I.e., \(\frac{\Delta \lambda}{\lambda}\)
For particular absorption or emission lines
Like the beautiful red \(H_{\alpha}\) line, for which the lab wavelength is \(\lambda=656.27\) nanometers.
original (unshifted) wavelength
i.e., in the lab on Earth
The wavelengths of the absorption lines can be measured accurately, however, and their Doppler shift is relatively simple to detect.
absorption OR emission lines can display redshift and blueshift
Solving this equation for the velocity
This is also the equation programmed into a policeman's radar gun, for measuring the speed \(v\) of speeders.
the wavelength emitted by the source
This means, as emitted by the source if it were in a stationary laboratory.
\(\Delta \lambda=\left(\lambda_{lab}-\lambda_{observed}\right)\)
So \(\frac{\Delta \lambda}{\lambda}\) is the percent change in wavelength.
Similar expressions exist for frequencies \(f_{lab}\) and \(f_{observer}\)
describe changes in the wavelengths of radio waves or X-rays
So a radio wave that has a smaller frequency than normal is redshifted. An xray wave with a higher frequency is blueshifted... all of this even though we do not perceive radio or xray as having color.
Color Shifts
This is the main concept to focus on, for Doppler shifting. Redshift and blueshift are commonly used tools for studying galaxy clusters, galaxies, stars, planets and even atoms.
Volcanoes
There are tons of volcanoes in the solar system. The largest volcano we know of is on Mars!!
This is the way many, but not all, of the mountain ranges on Earth were formed.
Another example: the Himalayas. They formed when the subcontinent of India bashed northward into Eurasia.
astronomy exams
Hmmmm...
It is a cooling system for the planet.
Convection!!
Heat escaping from the interior provides energy for the formation of our planet’s mountains, valleys, volcanoes, and even the continents and ocean basins themselves.
Main source of forces and motion = convection. Huge blobs of molten lava convect from core to surface, like water boiling in a pot on the stove or a thunderstorm convecting water vapor and liquid water in the atmosphere.
white
or pinkish up in Georgia!!!!
To find primitive rock, we must look to smaller objects such as comets, asteroids, and small planetary moons
Yup -- asteroids and comets are chunks of history going all the way back.