hockey

plausible

prominent

endorsements

Statute

pub game

linear combination of theksolutions

omogeneous linearrecurrence relation

non-homogeneous linearrecurrence relation

derivative

quotient formal powerseries

formal power series

multiplication rule

generating function

characteristic polynomial

FCFS

response time

t0      t1      P       cpu             queue
0       1       P2      busy                
1       2       -       cs              [P1]
2       7       P1      busy                
7       8       -       cs              [P4,P5,P3]
8       10      P4      busy
10      11      -       cs              [P5,P3]
11      14      P5      busy
14      15      -       cs              [P3]
15      19      P3      busy

total response time: (1-0) + (7-2) + (10-4) + (14-7) + (19-8) = 30

response time

t0      t1      P       cpu             queue
0       1       -       cs              [P2]
1       2       P2      busy                
2       3       -       cs              [P1]
3       6       P1      busy                
6       7       -       cs              [P4,P1,P5]
7       9       P4      busy
9       10      -       cs              [P1,P5,P3]
10      12      P1      busy
12      13      -       cs              [P5, P3]
13      16      P5      busy                
16      17      -       cs              [P3]
17      20      P3      busy
20      21      -       cs              [P3]
21      22      P3      busy

total response time: (2-0) + (12-2) + (9-4) + (16-7) + (22-8) = 40

finish time - the arrival time

exerted on

shear stress

Random Walks and Electric Networks

Use forward difference approximation. Cannot use central difference approximation

Dirichlet boundary condition

Neumann boundary condition

Lagrange Interpolating Polynomials

meshgrid

Multidimensional integration

Gauss Elimination - Pitfalls

STABILITY OF CRANK-NICOLSON

So the local truncation error for Crank-Nicolsonformula is and the global truncation error

ACCURACY OF CRANK-NICOLSON

Crank-Nicolson

Crank-Nicolson formula

4th order Runge Kutta

2nd order Runge Kutta

ΣBPA

Derivedoperators

satisfaction

Book

Gravity currents: a personal perspective

approximate the first derivatives

Numerical Methods for Engineers

A (2, 5)

Applied Numerical Methods Using MATLAB”

parts of speech

for each edge at most one of its endpoints is in S

Further, especially when getting into nonlinear filtering, if the state information is not perfect,but the uncertainty is set to 0 (or just too small a value) it might cause the filter to be unstable.

xk

incident to some vertex

meteorites

Binary-to-Gray

Gray Code

expression

Markov chain with the same boundary values.

This current is

flowing into

first->second

key, Value()

Node::operator new (size_t size, size_t numPointers)

A-instruction

which stores the last operationfrom thesametransaction

status:

a sequence of log records

how a database can abort a transaction

what inequality must hold

prevLSN

crease by 10 each time

two rules

Durability

The Strategy Pattern defines a family of algorithms, encapsulates each one, and makes them interchangeable. Strategy lets the algorithm vary independently from clients that use it.

Favor composition over inheritance.

Full Speed USB connector (USB0)

splinters

block size

The stator, or stationary part of the stepping motorholds multiple windings. The arrangement of thesewindings is the primary factor that distinguishesdifferent types of stepping motors from an electricalpoint of view.

variable reluctance

stator

rotor

Brushless

The ADC converts an analog input voltage to a 10-bit digital value through successive approximation.

The ADC contains a Sample and Hold circuit which ensures that the input voltage to the ADC is held at a constant level during conversion.

0x08

references

perform several orders in as many days

purchases

swellhead

Groups

singles

long play

flamethrower

gas can

deadly

a pit

landmines

metallic box

amateur

Penelope Dolittle

any word beginning with an upper-case letter is a Prolog variable

This is the way logical conjunction is expressed in Prolog (that is, the comma means and )

the semicolon ; is the Prolog symbol for or

the potency of a substance in inhibiting a specific biological or biochemical function

inhibitory concentration

kd-tree

Microprocessor

In certain databases the key values may be points in some multi-dimensional space

arity

it is usual to use a suffix / followed by a number to indicate the predicate’s arity

2.2.1 Pinhole Camera Model

2.2.2 Absolute Conic

the :- means implication, the , means conjunction, and the ; means disjunction

This will introduce us to the three basic constructs in Prolog: facts, rules, and queries.

network *net = make_network(sections->size - 1);

get_network_output_layer

net->outputs = out.outputs;

train_networks

train_network

get_current_batch

net->subdivisions

get_current_batch

Enter a directory where you’d like to store your code and run: scrapy startproject tutorial

we want the attribute href

How big is your cache block

How much data fits in the WHOLE cache

Your processor must provide the following outputs

Your processor has 2 inputs

Layer notation for convolutional neural networks

The __thiscall calling convention is used on member functions and is the default calling convention used by C++ member functions that do not use variable arguments.

Calling Conventions

Qt Widgets

Qt add-ons

Qt essentials

There are a few different options to run GUI applications inside a Docker container like using SSH with X11 forwarding, or VNC but the simplest one that I figured out was to share my X11 socket with the container and use it directly.

docker run -ti --rm \
       -e DISPLAY=$DISPLAY \
       -v /tmp/.X11-unix:/tmp/.X11-unix \
       firefox

2/3" (~ 8.8 x 6.6 mm)

math.atan(8.8 / 2 / 2.8) * 180 / math.pi * 2

Floating Point Calling Conventions

CPU Registers

The supported data types are as follows

Comments

Parameter Passing

Floating Point Instructions

The idea of the numeric_limits<T> trait class is due to John Barton and Lee Nackman

Structural Pattern Recognition

Algorithms for Graphics and Image Processing

Theo Pavlidis' Algorithm

 Borodovsky  &  Ekisheva  (2006),

What  is  the  probability  P(S)  that  this  sequence  S  was  generated  by  the  HMM  model?

Viterbi  algorithm

HMM  :  Viterbi  algorithm  -­a  toy  example

On the "IPv4 Settings tab", select Method: "Shared to other computers"

two cate-gories.

Pieter Abbeel

Johan Löfberg

YALMIP

Dr. Xiang Gao

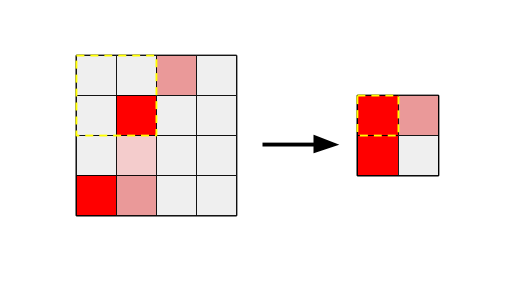
This shrinkage also means that the number of position variations that are possible has shrunk a lot.

Joan Bruna

You need 1,000 representative images for each class.

Machine Learning at UofT

a revolutionary technique(expression tem-plates,invented independently by Todd Veldhuizen-'' andDavid Vandevoorde") could be used to improve dramaticallythe runtime efficiency of high-level C++ code like sumlt.

Beating the Abstraction Penalty in C++ Using Expression Templates,

DisambiguatedGlommableExpressionTemplates