“Nice” “Cool” “Ok” If you get a lot of single word answers, you are not keeping the other person interested. They are trying to prevent you from saying more, either because you habitually talk too much or because the topic isn’t interesting to them.
Avoid single word answers
I have a friend who has somewhat extreme political views, but he will always say things like, “I believe X, but I bet you believe Y and you always have interesting takes, so I’d love to hear your thoughts”. It’s a great way to disagree in a positive and constructive way, and I always enjoy conversations with him.
It seems that these days everyone is so focused on being right and believes that changing their mind shows weakness, but in reality it is the opposite. Only confident people feel are able to change positions without affecting their self image.
Factual questions are good, but questions that deepen the conversation are even better. “What were you thinking when she said that?” “Was that as hard as it sounds?” “How did you learn how to do that?” “What made you decide to go that route?”
Try to ask questions that deepen the conversation
An ideal conversation is a mix of listening, asking questions, and sharing in a way that allows the other person to politely guide the conversation. You must ask questions so that the other person knows that you are interested in them and what they are saying. The worst conversations are those where both parties are waiting their turn to talk, saying as much as they can before getting interrupted, and then being forced to listen to the other.
Worst and best conversation types
I could tell a story about building my pinball machine. A crafty technical friend might be very interested in hearing every step, but my mom might not be interested in more than about 10 seconds of detail on it.
Pay attention how you share your information, and to whom
A conversation is best when both parties are interested, engaged, and want to share. If you interrupt you show that you are uninterested and you blunt the other person’s motivation to share.
Don't interrupt
I asked why she thought that was happening, and she said, “Covid”. The lack of socialization, especially at such a key time in life, had made this incoming class the first one that lacked basic manners and social skills.
Covid has heavily impacted our social/communication skills
This sort of behavior puts a huge burden on the listener because it makes them responsible for your emotional state. Their options are to deny you the emotional state you want, or to give it to you by lying. This is exhausting and will cause people to limit the amount of social time they spend with you.
Pay attention what you're sharing with different people, as not everyone will feel comfortable with receiving the same information
Nature 613, 19-21 (2023)
innovation communications tactics such as:• Building visibility with “tips from the lab” newsletters, blogs, guides, or tools. Skip the jargon. Put something tangible into the hands of staff.• Helping managers by creating team briefs, case studies and articles for team meetings.• Inviting executives for briefings to build your pool of champions.• Packaging presentations for staff meetings and manager conferences.• Creating basic education programs to help staff and teams solve problems on the job.
A good list of tactics to communicate about innovation. For example,
One could also think about a "virtual innovation" lab approach ...
Government policy innovationPublic services innovation (including service design and digital)Science and technology — governments employ thousands of scientists, engineers and researchers. Labs can think of ways for them to become more effective.Management systems innovation — “innovate” how government innovates to build skills, capacity and culture.
The article speaks about that "Management systems innovation" -- the way howe we build skills, capacity and culture -- is a key element for successful attempts for governments to innovation.
Concentrating on these aspects -- howe we work together, how we develop skills and capacity -- might be the key ingredients for a future for the OpenLab -- and the future of the innovation activities.
Maybe we could start offering "services" from the "OpenLab" to managers and teams ...?
Because I am as interested in the attitudes and assumptions which are implicit in the evidence as in those which were explicitly articulated at the time, I have got into the habit of reading against the grain. Whether it is a play or a sermon or a legal treatise, I read it not so much for what the author meant to say as for what the text incidentally or unintentionally reveals.
Historians, sociologists, anthropologists, and surely other researchers must often "read against the grain" which historian Keith Thomas defines as reading a text, not so much for what the author was explicitly trying to directly communicate to the reader, but for the small tidbits that the author through the text "incidentally or unintentionally reveals."
The “linguistic turn” in the social sciences focused on the socially constructed nature of “reality” (Berger & Luckmann 1979). With this turn, the focus was on the role of language as both describing and construing our understanding of what takes place in society. This means that we cannot assume that language (such as it is produced, for instance, in policy documents, legislation, parliamentary debates, interviews, etc.) merely describes reality; it also construes the ways in which we understand and conceptualise that (social) reality. Another implication of the linguistic turn in the social sciences is that policy texts cannot and should not be dismissed as “mere rhetoric”, with little to do with “real policy” (Saarinen 2008).
Modern science is, to a large extent, a model-building activity. In the natural and engineering sciences as well as in the social sciences, models are constructed, tested and revised, they are compared with other models, applied, interpreted and sometimes rejected or replaced by a better model.
Weaver distinguishes ‘three levels of communication problems’, beginning with the technical problem (A), which is concerned with the f idelity of symbol transmission and thus the level where Shannon’s mathematical def inition and measure of information are situated. But Weaver then also postulates a semantic problem (B) that refers to the transmission of meaning and an ef fectiveness problem (C) that asks
Three levels of communication problems: technical problem, semantic problem, and effectiveness problem. (Shannon and Weaver. 1964. A Mathematical Theory of Communication)
Tools for better thinking Collection of thinking tools and frameworks to help you solve problems, make decisions and understand systems.
<small><cite class='h-cite via'>ᔥ <span class='p-author h-card'>Howard Rheingold</span> in Howard Rheingold: "Y'all know about "Tools for …" - Mastodon (<time class='dt-published'>11/13/2022 17:33:07</time>)</cite></small>
Looks similar to Project Zero https://pz.harvard.edu/thinking-routines
The paradox of information systems[edit] Drummond suggests in her paper in 2008 that computer-based information systems can undermine or even destroy the organisation that they were meant to support, and it is precisely what makes them useful that makes them destructive – a phenomenon encapsulated by the Icarus Paradox.[9] For examples, a defence communication system is designed to improve efficiency by eliminating the need for meetings between military commanders who can now simply use the system to brief one another or answer to a higher authority. However, this new system becomes destructive precisely because the commanders no longer need to meet face-to-face, which consequently weakened mutual trust, thus undermining the organisation.[10] Ultimately, computer-based systems are reliable and efficient only to a point. For more complex tasks, it is recommended for organisations to focus on developing their workforce. A reason for the paradox is that rationality assumes that more is better, but intensification may be counter-productive.[11]
From Wikipedia page on Icarus Paradox. Example of architectural design/technical debt leading to an "interest rate" that eventually collapsed the organization. How can one "pay down the principle" and not just the "compound interest"? What does that look like for this scenario? More invest in workforce retraining?
Humans are complex, adaptive systems. Machines have a long history of being complicated, efficient (but not robust) systems. Is there a way to bridge this gap? What does an antifragile system of machines look like? Supervised learning? How do we ensure we don't fall prey to the oracle problem?
Baskerville, R.L.; Land, F. (2004). "Socially Self-destructing Systems". The Social Study of Information and Communication Technology: Innovation, actors, contexts. Oxford: Oxford University Press. pp. 263–285
Topic: Communication with the Zettelkasten: How to get an adequate partner, junior partner? – important after working with staff becomes more and more difficult and expensive. Zettel’s reality
The best and most challenging communication partner you may experience is a version of your past self. A searchable set of notes is the closest approximation of this one is likely to find.
Von Bu ̈ low and Krusche analyze this system as a medium of “conversationwith oneself,” where the Zettelkasten stands in for lacking or absent inter-locutors.19
They write this, but was it before or after Luhmann wrote his essay on Communication with the Slip Box to suggest the idea? Presumably there was heavy influence here.
This is not "noise"
2 advantages of communicating on group channels instead of using DMs
But having a conversation partner in your topic is actually ideal!
What's the solution: dig into your primary sources. Ask open-ended questions, and refine them as you go. Be open to new lines of inquiry. Stage your work in Conversation with so-and-so [ previously defined as the author of the text].
Stacy Fahrenthold recommends digging into primary sources and using them (and their author(s) as a "conversation partner". She doesn't mention using either one's memory or one's notes as a communication partner the way Luhmann does in "Kommunikation mit Zettelkästen" (1981), which can be an incredibly fruitful and creative method for original material.
Quicker And More Useful Communication
Great example of asking precise questions
Rothmund, T., Farkhari, F., Azevedo, F., & Ziemer, C.-T. (2020). Scientific Trust, Risk Assessment, and Conspiracy Beliefs about COVID-19—Four Patterns of Consensus and Disagreement between Scientific Experts and the German Public. PsyArXiv. https://doi.org/10.31234/osf.io/4nzuy
Notion – The all-in-one workspace for your notes, tasks, wikis, and databases. (n.d.). Notion. Retrieved 14 February 2022, from https://www.notion.so
Rebitschek, F., Ellermann, C., Jenny, M., Siegel, N. A., Spinner, C., & Wagner, G. (2021). How skeptics could be convinced (not persuaded) to get vaccinated against COVID-19. PsyArXiv. https://doi.org/10.31234/osf.io/f4nqt
ReconfigBehSci. (2021, December 7). RT @jitsuvax: 🇵🇱NEW translation of the Covid-19 Handbook for our friends in Poland https://c19vax.scibeh.org/pl This work was only possible beca… [Tweet]. @SciBeh. https://twitter.com/SciBeh/status/1468247395070885907
ReconfigBehSci [@SciBeh]. (2021, August 6). The pathologies of science Twitter are on full display in this thread featuring a non-expert blasting an epidemiologist for “stealing” an idea (a minor statistical insight) that is part of epidemiological basic understanding [Tweet]. Twitter. https://twitter.com/SciBeh/status/1423688923348299781
Tom Lawton. (2022, January 10). 🔹99.995% of people who drank from that pump didn’t die. 🔹We need to learn to live with the dirty water. 🔹Dirty water is fine to drink if you don’t have underlying health conditions. 🔹It’s not necessary to clean the water unless it’s wholly waterborne. (/S!) [Tweet]. @LawtonTri. https://twitter.com/LawtonTri/status/1480502910459039749
Why did some conversations unfurl and others wilt? One answer, I realized, may be the clash of take-and-take vs. give-and-take.
This is a remarkable analysis. If it holds water, it's easy to grasp and helpful to apply.
GPT-3 is by no means a reliable source of knowledge. What it says is nonsense more often than not! Like the demon in The Exorcist, language models only adds enough truth to twist our minds and make us do stupid things
The need to be aware that GPT-3 is a text generation tool, not an accurate search engine. However being factually correct is not a prerequisite of experiencing surprisal. The author uses the tool to open up new lines of thought, so his prompt engineering in a way is aimed at being prompted himself. This is reminiscent of how Luhmann talks about communicating with his index cards: the need for factuality does not reside with the card, meaning is (re)constructed in the act of communication. The locus of meaning is the conversation, the impact it has on oneself, less the content, it seems.
https://web.archive.org/web/20220810205211/https://escapingflatland.substack.com/p/gpt-3
Blogged a few first associations at https://www.zylstra.org/blog/2022/08/communicating-with-gpt-3/ . Prompt design for narrative research may be a useful experience here. 'Interviewing' GPT-3 a Luhmann-style conversation with a system? Can we ditch our notes for GPT-3? GPT-3 as interface to the internet. Fascinatiing essay, need to explore.
Later in life and irrespective to the character of the relationship held, the good enough approachinforms how communication between people can be practiced. One of the widest known formulasfor that is called Nonviolent Communication, subtitled as the ‘language of life’ [ 39]. The subtitle seemsparticularly appropriate to our case, as it describes a method of communication that does not servesocial programming and allow humans to author and own their speech. A nonviolent communicatordoes not reinforce the boundary cuts and refrains from installing the personware-shaping doublebinds.
!- definition : nonviolent communication, language of life * a method of communication that does not prioritize social programming over an individual's right to articulate and own their own speech.
So we end up with the problem usually referred to as ‘information overload’ but I prefer to call notification literacy. As I say in the linked post, there are preventative measures and mitigating actions you can take as an individual to help ‘increase your notification literacy’. There are also ways of facilitating communities that can help, for example if the platform you’re using has threaded comments, insisting that people use instead of a confusing, undifferentiated stream of messages. You can also ensure you have a separate chat or channel just for important announcements.
First, while using the previous retrieval methods, it is a good ideato keep your focus a little broad. Don’t begin and end your searchwith only the specific folder that matches your criteria.
The area of serendipity becomes much more powerful when one has ideas both directly interlinked, ideas categorized with subject headings or tags, or when one can have affordances like auto-complete.
The method Forte suggests and outlines allows for some serendipity, but not as much as other methods with additional refinements. Serendipity in Forte's method isn't as strong as in others.
In this section he's talking about some of the true "magic of note taking" which is discussed by Luhmann and others.
link to:<br /> Luhmann's writings on serendipity and surprise when using his zettelkasten (Communication with the Slipbox...)<br /> Ahrens mentions of this effect
The Antinet’s permanent-address scheme, with its shifting nature, gives the system a unique personality. The Antinet’s unique personality stands as one of the most integral aspects of the system. A key component that enables insightful communication with a human being is the human’s personality–the person’s unique way of communicating with you based on their unique perspectives and interpretations. The Numeric-alpha addresses provide the Zettelkasten with a unique personality. Over time, unique structures form due to Numeric-alpha addresses. This is important because it allows one to communicate with the Antinet, transforming it into a communication experience with a second mind, a doppelgänger, or a ghost in a box, as Luhmann called it. (5)5 This is the entity Luhmann referred to when he titled his paper, Communicating with Noteboxes. Numeric-alpha addresses make all of this possible.
Scheper seems to indicate that it is the addressing system alone which provides the "personality" of a zettelkasten, whereby he's actively providing personification of a paper and pencil system by way of literacy. We need to look more closely, however at the idea of what communication truly is to discern this. A person might be able to read an individual card and have a conversation with just it, but this conversation will be wholly one sided, and stops at the level of that single card. We also need the links between that individual card and multiple others to fill in the rest of the resulting potential conversation. Or we will rely on the reader of the card extending the idea or linking it to others of their ideas (and that of the zettelkasten), to grow the system and thereby its "personality".
Thus the personality is part that of the collection of cards using their addresses and the links between them. This personality, however, isn't immediate. It might grow over time reaching some upper limit at the length of time of the user's life, but much of its personality is contingent upon the knowledge of the missing context of the system that is contained in or by its creator. Few zettelkasten will be so well composed as to provide full context. (cross reference: https://hyp.is/5gWedOs7Eeyrg2cTFW4iCg/niklas-luhmann-archiv.de/bestand/Zettelkasten/zettel/ZK_2_NB_9-8_V).
The question we might want to look at: Is there a limiting upper bound (a la a Shannon Limit) to the amount of information that a zettelkasten might contain or transmit, even beyond the life of an initial creator? Could it converse with itself without the assistance of an outside actor of some sort? What pieces are missing that might help us to define communication or even life itself?
“ Communication is . . . autopoietic insofar as it can only beproduced in a recursive relationship to other communications, that is to say, only in anetwork, to the reproduction of which each individual communication contributes.”42
- Luhmann, Die Gesellschaft der Gesellschaft , 82f.
Communication “is the smallest possible unit of a social system,namely that unit to which communication can still react through communication.”40
- Luhmann, Die Gesellschaft der Gesellschaft , 82.
Unfortunately, there were more cases in 2018 than in 2017 (29 versus 22).
The numbers and rosy picture here aren't quite as nice as other—more detailed—reporting in the Economist recently would lead us to believe.
In some sense I do appreciate the sophistication of Bill Gates' science communication here though as I suspect that far more Westerners are his audience and a much larger proportion of them are uninformed anti-vaxxers who might latch onto the idea of vaccine-derived polio cases as further evidence for their worldview of not vaccinating their own children and thereby increasing heath risk in the United States.
Projects like the Open Journal System, Manifold or Scalar are based on a distributed model that allow anyone to download and deploy the software (Maxwell et al., 2019), offering an alternative to the commercial entities that dominate the scholarly communication ecosystem.
Might Hypothes.is also be included with this list? Though it could go a bit further toward packaging and making it more easily available to self-hosters.
emancipatory communication seeks “to circumvent the politics of enclosure and control enacted by states, regulators, and corporations” (Milan, 2019 , p. 1)
Having been printed on paper since the very first scientific journal was inaugurated in 1665
There is some history here. The first scientific journal was one that published the proceedings of one of the first scholarly society meetings (The (mostly true) origins of the scientific journal - Scientific American Blog Network) and resulting letters.
Institutions may supply learning environments that facilitate social interaction and collaboration and assure effective support to students with technological difficulties. Technological difficulties can cause student frustration as well as communication problems, which hamper collaborative processes such as explanations, sharing answers, and negotiation (Ragoonaden & Bordeleau, 2000).
difficulties with regard to communication as another source of frustration. Communication was reported to be essential in keeping group members focused on their responsibilities in relation to the common goal
difficulties in communication
ReconfigBehSci. (2022, January 24). Interesting SciComm on Twitter development- the dedicated translator [Tweet]. @SciBeh. https://twitter.com/SciBeh/status/1485700178871046144
ReconfigBehSci [@SciBeh]. (2021, November 14). @STWorg @olbeun @lombardi_learn @kostas_exarhia @stefanmherzog @commscholar @johnfocook @Briony_Swire @Sander_vdLinden @DG_Rand @kendeou @dlholf @ProfSunitaSah @HendirkB @gordpennycook @andyguess @emmapsychology @ThomsonAngus @UMDCollegeofEd @gavaruzzi @katytapper @orspaca [Tweet]. Twitter. https://twitter.com/SciBeh/status/1459813535974842371
ReconfigBehSci [@SciBeh]. (2021, October 13). transparent public discourse is not easy, nor automatic. We need better tools, better community norms, and, generally, a better understanding of online discourse http://SciBeh.org [Tweet]. Twitter. https://twitter.com/SciBeh/status/1448305801446105088
ReconfigBehSci [@SciBeh]. (2021, November 14). Kai Spiekermann will speak the need for science communication and how it supports the pivotal role of knowledge in a functioning democracy. The panel will focus on what collective intelligence has to offer. 3/6 [Tweet]. Twitter. https://twitter.com/SciBeh/status/1459813528987217926
Dr Dominic Pimenta [@DrDomPimenta]. (2021, December 15). An illustration of communicating risk with “less severe” variants: [Thread] Assume Omicron is 4x more transmissible than Delta. [1] Assume Omicron leads to 1/3 less admissions than Delta. [Figure below] Assume 1 in 100 cases of Delta are admitted to hospital. Https://t.co/XtnVwoOrUo [Tweet]. Twitter. https://twitter.com/DrDomPimenta/status/1471094002808242177
ReconfigBehSci. (2020, November 25). @ToddHorowitz3 @sciam do you mean the specific article is bad, or the wider claim/argument? Because as someone who does research on collective intelligence, I’d say there is some reason to believe it is true that there can be “too much” communication in science. See e.g. The work of Kevin Zollman [Tweet]. @SciBeh. https://twitter.com/SciBeh/status/1331672900550725634
ReconfigBehSci on Twitter: ‘Now #scibeh2020: Pat Healey from QMU, Univ. Of London speaking about (online) interaction and miscommunication in our session on “Managing Online Research Discourse” https://t.co/Gsr66BRGcJ’ / Twitter. (n.d.). Retrieved 6 March 2021, from https://twitter.com/SciBeh/status/1326155809437446144
ReconfigBehSci. (2020, November 10). Now #scibeh2020: Presentation and Q&A with Martha Scherzer, senior risk communication and community engagement (RCCE) Consultant at the World Health Organization https://t.co/Gsr66BRGcJ [Tweet]. @SciBeh. https://twitter.com/SciBeh/status/1326148149870809089
Amy Maxmen, PhD. (2020, August 26). 🙄The CDC’s only substantial communication with the public in the pandemic is through its MMW Reports. But the irrelevant & erroneous 1st line of this latest report suggests political meddling to me. (The WHO doesn’t declare pandemics. They declare PHEICs, which they did Jan 30) https://t.co/Y1NlHbQIYQ [Tweet]. @amymaxmen. https://twitter.com/amymaxmen/status/1298660729080356864
Stefan Simanowitz. (2021, March 18). 1/. The PM claims that the govt “stuck to the science like glue” But this is not true At crucial times they ignored the science or concocted pseudo-scientific justifications for their actions & inaction This thread, & the embedded threads, set them out https://t.co/dhXqkSL1bz [Tweet]. @StefSimanowitz. https://twitter.com/StefSimanowitz/status/1372460227619135493
Adam Kucharski. (2020, December 13). I’ve turned down a lot of COVID-related interviews/events this year because topic was outside my main expertise and/or I thought there were others who were better placed to comment. Science communication isn’t just about what you take part in – it’s also about what you decline. [Tweet]. @AdamJKucharski. https://twitter.com/AdamJKucharski/status/1338079300097077250
ReconfigBehSci on Twitter: ‘many aspects to the vaccine pauses are worthy of discussion, but am I alone in thinking that undermining public perception of the regulators can only increase vaccine hesitancy? Can promoting trust in vaccine safety by publicly condemning decision really be a viable strategy?’ / Twitter. (n.d.). Retrieved 17 March 2021, from https://twitter.com/SciBeh/status/1372142352941379584
Stephan Lewandowsky. (2021, September 20). Major update to the wiki underlying our COVID-19 Vaccination Communication Handbook https://sks.to/c19vax 1/n https://t.co/gosByQsg4y [Tweet]. @STWorg. https://twitter.com/STWorg/status/1439854554477105162
ReconfigBehSci. (2021, November 14). Join us this week at our 2021 SciBeh Workshop on the topic of ‘Science Communication as Collective Intelligence’! Nov. 18/19 with a schedule that allows any time zone to take part in at least some of the workshop. Includes: Keynotes, panels, and breakout manifesto writing 1/6 [Tweet]. @SciBeh. https://twitter.com/SciBeh/status/1459813525635973122
ReconfigBehSci. (2021, November 14). Deepti Gurdasani will share insights from her experience as a science communicator on Twitter in the pandemic. And the panel will discuss how we can build and sustain systems—Particularly online spaces—That can support the role of collective intelligence in Sci Comm 5/6 [Tweet]. @SciBeh. https://twitter.com/SciBeh/status/1459813532149637121
ReconfigBehSci. (2021, November 18). reports of Covid “parties” and resultant deaths from Austria. This presumably is a potential reason for why policy might chose to not treat recovery as equivalent to vaccination where restrictions based on status are in place (e.g., 2G,3G in Germany and Austria) https://t.co/xH3btENi4X [Tweet]. @SciBeh. https://twitter.com/SciBeh/status/1461013914792169478
It feels great to get an email from someone you care about. Or a newsletter you enjoy. Or an update from a service you like. That’s how email used to feel all the time.
Email gets a bad rap, but it shouldn’t. Email’s a treasure.
4 - Distribution de documents aux familles : Comme l’institution scolaire se doit de protéger la liberté de conscience et l’identité de chacun des élèves dont elle a la charge, la distribution de documents informatifs, qui pourraient être considérés comme pouvant entraver ce principe de neutralité, peut être faite aux familles sans qu’elle ne puisse être directement accessible aux élèves, et donc jamais collés dans les cahiers de liaisons. Cela peut se faire : -sous pli cacheté, fermé ou agrafé (aucun texte visible). de main à la main à la sortie de la classe.
cela ne concerne pas les représentants de parents mais les pro à mon sens. et c'est un peut limite quant au respect de neutralité
Le travail matériel préalable et notamment la présentation des documents en plis clos ou agrafés doivent être assurés par les associations.
circulaire n°88-208 du 29/8/88
Note- Taking as Information Management
cross reference her paper:
Blair, Ann. “Note Taking as an Art of Transmission.” Critical Inquiry 31, no. 1 (September 2004): 85–107. https://doi.org/10.1086/427303.
Redistribution can easily become a bottleneck due to the bandwidthof cross-device links usually being magnitudes smaller than that of the on-device memory bus.
redistribution arrays 可能会遇到什么问题？
Modern large-scale deep learning workloads highlight the need for parallel execution across many devicesin order to fit model data into hardware accelerator memories. In these settings, array redistribution maybe required during a computation, but can also become a bottleneck if not done efficiently
为什么需要 array redistribution?
Brianna Wu. (2021, June 5). MRNA is unbelievably fragile. The enzymes that degrade it are literally everywhere. That’s why they had to develop specialized lipid nanoparticles to deliver it. It would last two seconds in a sewer system. Also, it gets separated from the delivery system after it’s injected. Https://t.co/35dZ6r6UAq [Tweet]. @BriannaWu. https://twitter.com/BriannaWu/status/1400998163968933888
COVID-19 Vaccination Field Guide: 12 Strategies for Your Community-. (n.d.). 48.
ReconfigBehSci. (2021, November 20). Thanks to everyone who took part in our Workshop on #SciComm as Collective Intelligence It was amazing! Materials will be uploaded to http://SciBeh.org website 1/2 @kakape @DrTomori @SpiekermannKai @GeoffreySupran @ArendJK @STWorg @dgurdasani1 @suneman @philipplenz6 [Tweet]. @SciBeh. https://twitter.com/SciBeh/status/1461978072924762117
Harp, N., Langbehn, A. T., Larsen, J., Niedenthal, P., & Neta, M. (2022). Facial coverings differentially alter valence judgments of emotional expressions. PsyArXiv. https://doi.org/10.31234/osf.io/5a9fd
ReconfigBehSci. (2022, March 14). RT @jitsuvax: Https://hackmd.io/@scibehC19vax/home Short update to the @jitsuvax and @SciBeh COVID-19 Communication Handbook. 🥪 Using the Fact-Sandwich… [Tweet]. @SciBeh. https://twitter.com/SciBeh/status/1503641642129145857
but i i think the first couple of hundred notes are more like a collection and you look 00:34:29 for um connections and there are some but you remember them because yes the amount where it's where it doesn't surprise you 00:34:43 uh it's more you know where they are and i think the from 500 on um there's a shift um and then you need to uh figure out how to um 00:34:58 find them again so the index or some kind of system becomes more important and i think a couple of thousand notes and uh you're 00:35:12 automatically turning to your set of custom [Music] as the place where you will likely find some kind of connection
Q: How many permanent notes did it take before you felt you had a communication partner?
Sönke Ahrens has indicated that the first couple hundred notes are more of a static collection. Then from five hundred notes onward there is a shift and having an index becomes more important. It's only at about one thousand notes that one begins automatically turning to the zettelkasten to find connections. Perhaps it's at this point that the tool begins to look like a communication partner.
link this to the few other examples from others.
Bad Vaccine Takes. (2022, January 26). This account is fake https://t.co/r5SXmzuPQj [Tweet]. @BadVaccineTakes. https://twitter.com/BadVaccineTakes/status/1486445924071129097
trust that research processes generate valid, useful knowledge and evidence that caninform practice and decision-making both within the HE context and in society morebroadly.
There is also an intersection here with the long-standing problems with for-profit corporate interests in the scholarly communication chain that are probably not addressed in this article.
Sinclair, Alyssa H., Morgan Taylor, Freyja Brandel-Tanis, Audra Davidson, Aroon T. Chande, Lavanya Rishishwar, Clio Maria Andris, et al. ‘Counteracting COVID-19 Risk Misestimation with an Interactive Website’. PsyArXiv, 9 February 2022. https://doi.org/10.31234/osf.io/v8tdf.
Gesturing also increases as afunction of difficulty: the more challenging the problem, and the more optionsthat exist for solving it, the more we gesture in response.
When presented with problems people are prone to gesture more with the increasing challenges of those problems. The more ways there are to solve a particular problem, the more gesturing one is likely to do.
What sort of analysis could one do on politicians who gesture their speech with relation to this? For someone like Donald J. Trump who floats balloons (ideas--cross reference George Lakoff) in his speeches, is he actively gesturing in an increased manner as he's puzzling out what is working for an audience and what isn't? Does the gesturing decrease as he settles on the potential answers?
Children can typically understand and act on a request to point to theirnose, for example, a full six months before they are able to form the spokenword “nose.”
Many children are also able to begin using sign language for their needs prior to being able to use spoken language as well.
Research shows that we all engage in such “gestural foreshadowing,” in whichour hands anticipate what we’re about to say.
Research by Christian Heath indicates that in interpersonal communication that speakers gesture meaning before they form the related words and listeners begin nodding at the gestures before they hear the spoken words.
All of us, then, are effectively bilingual: we speak one or more languages, butwe are also fully fluent in gesture.
I'm reminded of how Academy Award winning film editor Walter Murch once told me that his first edit of a feature film was always done without any sound at all. If the motions and actions of the actors could communicate as much meaning as possible, then the spoken words would only help to supplement the storytelling.
linguists theorize that gesture was humankind’searliest language, flourishing long before the first word was spoken
Evolutionarily speaking many animals communicate via gesture (body movements, tail wagging, etc.), so it isn't a far stretch to declare that linguists would consider gesture to be a precursor to language.
On other occasions,gesture supplies meaning that is not found anywhere in the speaker’s words
Gesture can supply contextual meaning of a speaker's meaning that isn't found in their spoken words.
What potential implications might this have to famous examples of visual versus non-visual communication, specfically: - The Kennedy/Nixon debates in which television and radio audiences had different perceptions of who won or lost. - Donald J. Trump's speeches where his politicobabble could be construed to mean almost anything to any listener, but his gestures may sway the meaning to a more concrete meaning.
gesture is often scorned as hapless“hand waving,” or disparaged as showy or gauche.
The value of gesture is sometimes disparaged with the phrase "handy waving".
Some of this statement is misleading as a hand waving argument relies solely on the movement of the hands as "proof" of something which is neither communicated well with the use of either words or the physical hand movements. The communication fails on both axes, but the blame is placed on the gestural portion of the communication, perhaps because it may have been the more important of the two?
Link this to the example of the Riverside teacher who used both verbal and visual gestures and acting to cement the trigonometry ideas of soh, cah, toa to her students and got fired for it. In her example, the gauche behaviour was overamplified by extreme exaggeration as well as racist expression.
“symbolic gestures”—movementsthat capture the overall meaning of the speaker’s message—along with what arecalled “beat gestures”: hand motions that serve to punctuate a particular point.
There are two broad types of gestures: - symbolic gestures: movements that help to capture the semantic meaning of one's message; - beat gestures which serve to punctuate one's points.
Are there other gesture types or classifications? Is there research on the perceived ability of actors who perform these techniques? What about small facial movements like eyebrows which may serve these functions as well.
Relate to micro facial movement research as means of communicating emotion.
Jean Clarke, a professor of entrepreneurship and organization at EmlyonBusiness School in France, has spent years watching entrepreneurs like GabrielHercule make their case at demo days, incubators, and investment forums acrossEurope. In a study published in 2019, she and her colleagues reported thatcompany founders who deployed “the skilled use of gesture” in their pitcheswere 12 percent more likely to attract funding for their new ventures.
Researcher Jean Clarke's research (2019) indicates that entrepreneurs who employ "the skilled use of gesture" are 12 percent more likely to have their pitches funded than those who don't.
Researchers who study embodiedcognition are drawing new attention to the fact that people formulate and conveytheir thoughts not only with words but also with the motions of the hands and therest of the body. Gestures don’t merely echo or amplify spoken language; theycarry out cognitive and communicative functions that language can’t touch.
Embodied cognition is a theory in psychology that a the mind is shaped by entire body of an organism. The mind is not only attached to the body, but the body influences the mind. Movement of the body doesn't just amplify one's spoke language, for humans, but it helps to create cognitive and communicative functions that language cannot, and these extend not only to viewers, but the communicator themself.
En somme, les études sur la communication des élèves atteints d’autisme permettent de mettre en évidence l’importance d’un contexte riche en stimulations appropriées (sons et images), mais également une évidente « stabilité » de l’information à décoder, le suivi des émotions des personnages, le rôle de l’imitation dans les apprentissages. Ces résultats encouragent donc l’usage d’outils informatiques adéquats pour améliorer la communication sociale chez les enfants atteints d’autisme.
L'association de deux sujets qui n'ont pas de corrélation vérifiéé, revient dans la conclusion en contradiction avec la conclusion de l'étude de Ramdoss, S et al.
Nous allons montrer par une courte analyse de quelques études l’impact du travail éducatif informatisé dans l’apprentissage de la communication sociale chez des enfants atteints d’autisme.
En contradiction avec l'hypothèse :
Results suggest that CBI should not yet be considered a researched-based approach to teaching communication skills to individuals with ASD. However, CBI does seem a promising practice that warrants future research. Les résultats suggèrent que le CBI ne devrait pas encore être considéré comme un approche fondée sur la recherche pour enseigner les compétences en communication aux personnes ayant Troubles du Spectre Autistique. Cependant, le CBI semble être une pratique prometteuse qui justifie des recherches futures.
Sometimes unclear bullshit is not merely temporarily unclear, but it is inherently unclear. This is the sort of bullshit that troubles G. A. Cohen. In his (2002) paper “Deeper into Bullshit,” he notes that bullshit does not merely involve seeking to more or less intentionally “mislead with respect to reality.” He argues that sometimes the content being produced has “unclarifiable unclarity” and Cohen wants to say that this is a key component of bullshit. On his view, bullshit statements are “not only obscure but cannot be rendered unobscured.”
Corporate apology, sunsetting statements after acquihires.
I also think that Marco Jacquemet is on point in his “45 as a Bullshit Artist” article, when he suggests that a lot of bullshit can be traced to violating the philosopher Paul Grice’s “Cooperative Principle.” What is that?There are actually two ideas from Grice that we can make use of. One idea is Grice’s distinction between what is literally said and what the person is attempting to communicate. In Grice’s terminology, there is a difference between the proposition expressed and the proposition meant. So, for example, Bill Clinton often literally said something true while attempting to communicate something quite false.
Also in the case of PR. “We all know getting a balanced diet is key to health, that’s why our sugary processed gloop is high in a single vitamin additive”
young companies typically fail because you have a charismatic leader with a bunch of beliefs, but those beliefs don't translate to the rest of their company
failure in communication
SciBeh Virtual Workshop 2021: Science Communication as Collective Intelligence. (n.d.). SciBeh. Retrieved 14 February 2022, from https://www.scibeh.org/events/workshop2021/
World Health Organization (WHO) on Twitter. (n.d.). Twitter. Retrieved 13 February 2022, from https://twitter.com/WHO/status/1485554889900142599
Singh, K., Lima, G., Cha, M., Cha, C., Kulshrestha, J., Ahn, Y.-Y., & Varol, O. (2022). Misinformation, believability, and vaccine acceptance over 40 countries: Takeaways from the initial phase of the COVID-19 infodemic. PLOS ONE, 17(2), e0263381. https://doi.org/10.1371/journal.pone.0263381
Dame Adjin-Tettey, T. (2022). Combating fake news, disinformation, and misinformation: Experimental evidence for media literacy education. Cogent Arts & Humanities, 9(1), 2037229. https://doi.org/10.1080/23311983.2022.2037229
Michaud, M., & Center, U. of R. M. (n.d.). Trust in science at root of vaccine acceptance. Retrieved February 8, 2022, from https://medicalxpress.com/news/2022-01-science-root-vaccine.html
Bjørkheim, Sebastian, and Bjørn Sætrevik. ‘Risk of Infection and Appeal to Public Benefit Increase Compliance with Infection Control Measures’. PsyArXiv, 12 January 2022. https://doi.org/10.31234/osf.io/myv4t.
Democracy in the age of social media. (n.d.). EXPeditions - Meet the World’s Best Minds. Retrieved February 5, 2022, from https://www.joinexpeditions.com/exps/43
I "communicate" with it when I tell it things like, "today, my throat was a little store."
This is not the same sort of "communication" with an external tool that Niklas Luhmann was talking about in Communicating with Slip Boxes.
R e c o m m a n d at i o n n ° 1 2 La Défenseure des droits recommande aux directeurs académiques, en concertation avec les collèges et lycées, de diffuser à chaque rentrée scolaire, via un support adapté (livret d’accueil, etc.), les informations relatives à la présence au sein de l’établissement, de l’assistante sociale et de l’infirmière scolaire. Une information systématique à destination des parents sur l’accès à la médecine scolaire doit aussi être organisée
Mackay, A. I. M. & PhD. (2022, January 29). Thank goodness we did all the work. Virology Down Under. https://virologydownunder.com/thank-goodness-we-did-all-the-work/
education has been moving farther and farther away from memorization-based learning. The standardized tests I give are modeled off of the AP History exams’ Document Based Questions, which prioritize analysis and communication skills over rote memorization.
Education has been moving farther away from memorization-based learning and instead prioritizing analysis and communication skills.
Story of a scientist trying to optimize for solutions of Wordle.
Nothing brilliant here. Depressing that the story creates a mythology around algorithms as the solution rather than delving in a bit into the math and science of information theory to explain why this solution is the correct one.
Desperately missing from the discussion are second and third order words that would make useful guesses to further reduce the solution space for actual readers.
Trust in Science is Changing. (n.d.). The Science Writer. Retrieved January 21, 2022, from https://www.thesciencewriter.org/uncharted/trust-science-changing
Should bad science be censored on social media? (2022, January 19). BBC News. https://www.bbc.com/news/technology-60036861
Yang, M. (2022, January 14). ‘Menace to public health’: 270 doctors criticize Spotify over Joe Rogan’s podcast. The Guardian. https://www.theguardian.com/technology/2022/jan/14/spotify-joe-rogan-podcast-open-letter
Carmody, D., Mazzarello, M., Santi, P., Harris, T., Lehmann, S., Abbiasov, T., Dunbar, R., & Ratti, C. (2022). The effect of co-location of human communication networks. ArXiv:2201.02230 [Physics, Stat]. http://arxiv.org/abs/2201.02230
Fischer, O., Jeitziner, L., & Wulff, D. U. (2021). Affect in science communication: A data-driven analysis of TED talks. PsyArXiv. https://doi.org/10.31234/osf.io/28yc5
McCrackin, S., Ristic, J., Mayrand, F., & Capozzi, F. (2021). Face masks impair basic emotion recognition: Group effects and individual variability (Accepted for Publication in Social Psychology). PsyArXiv. https://doi.org/10.31234/osf.io/2whmp
The fixed filing place needs no system. It is sufficient that we give every slip a number which is easily seen (in or case on the left of the first line) and that we never change this number and thus the fixed place of the slip. This decision about structure is that reduction of the complexity of possible arrangements, which makes possible the creation of high complexity in the card file and thus makes possible its ability to communicate in the first place.
There's an interesting analogy between Niklas Luhmann's zettelkasten numbering system and the early street address system in Vienna. Just as people (often) have a fixed address, they're able to leave it temporarily and mix with other people before going back home every night. The same is true with his index cards. Without the ability to remove cards and remix them in various orders, the system has far less complexity and simultaneously far less value.
Link to reference of street addressing systems of Vienna quoted by Markus Krajewski in (chapter 3 of) Paper Machines.
Both the stability and the occasional complexity of the system give it tremendous value.
How is this linked to the idea that some of the most interesting things within systems happen at the edges of the system which have the most complexity? Cards that sit idly have less value for their stability while cards at the edges that move around the most and interact with other cards and ideas provide the most value.
Graph this out on a multi-axis drawing. Is the relationship linear, non-linear, exponential? What is the relationship of this movement to the links between cards? Is it essentially the same (particularly in digital settings) as movement?
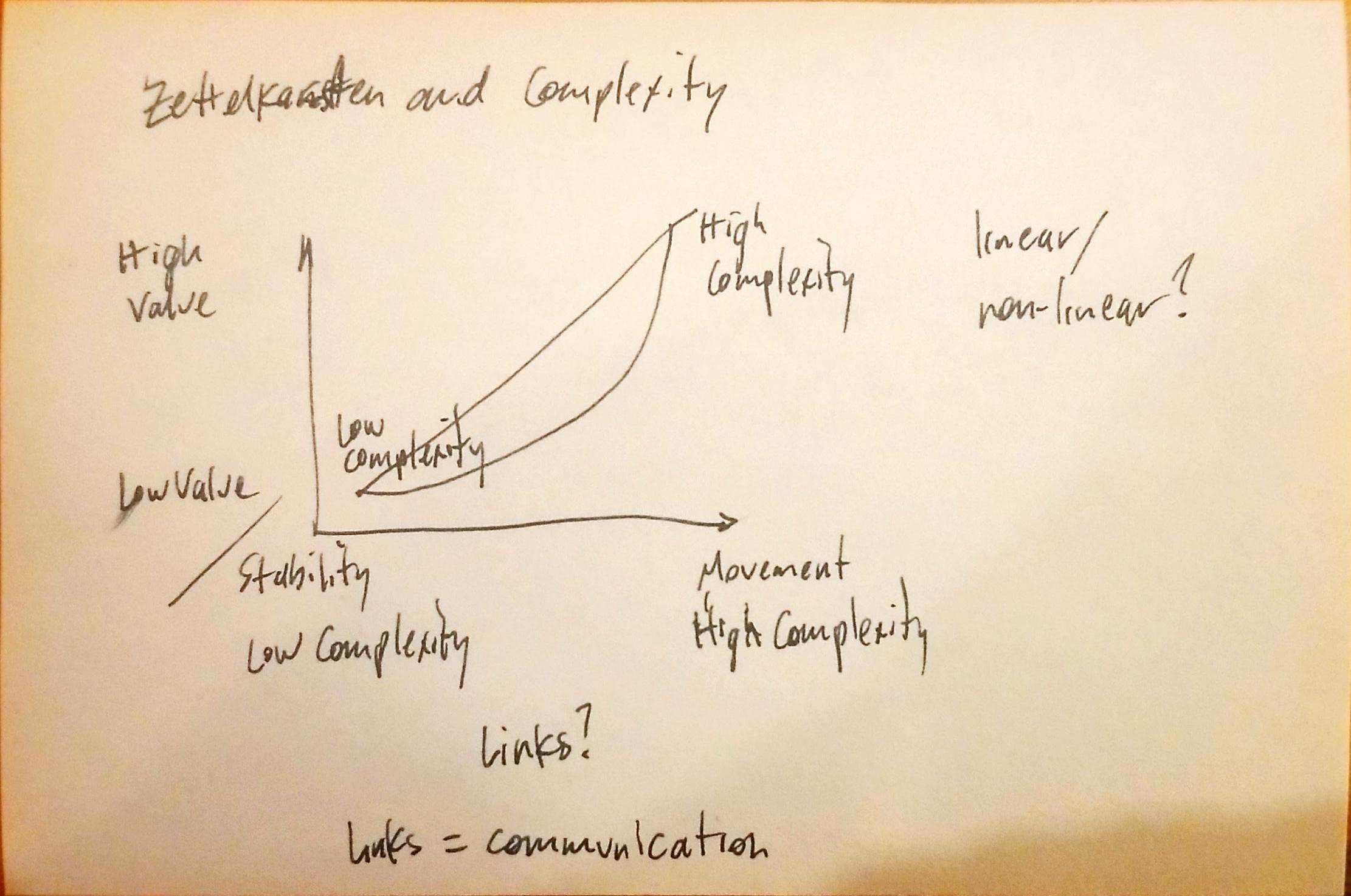
Are links (and the active creation thereof) between cards the equivalent of communication?
One of the most basic presuppositions of communication is that the partners can mutually surprise each other.
A reasonably succinct summary of Claude Shannon's 1948 paper The Mathematical Theory of Communication. By 1981 it had firmly ensconced itself into the vernacular, and would have done so for Luhmann as much of systems theory grew out of the prior generation's communication theory.
With secondary sources, I like to check and see what the author is doing with the information. It's standard to refer to interpretations that agree with yours, but often even more interesting when the new interpretation is arguing with, modifying, or "complicating" the previous one.
I have noticed in some anthropological literature that it appears that the authors completely missed the boat as the result of the lack of ability to communicate with their subjects or better understand their broader basic contexts.
Particular examples of this: -1930s: A. Irving Hallowell conversations with William Berens, Chief of the Berens River Anishinaabe about rocks
Courtney, D. S., & Bliuc, A.-M. (2021). Antecedents of Vaccine Hesitancy in WEIRD and East Asian Contexts. Frontiers in Psychology, 12, 5873. https://doi.org/10.3389/fpsyg.2021.747721
Schmid, P., & Lewandowsky, S. (n.d.). Tackling COVID disinformation with empathy and conversation. The Conversation. Retrieved December 15, 2021, from http://theconversation.com/tackling-covid-disinformation-with-empathy-and-conversation-173013
When the user stores his thoughts in his own filing cabinet, these thoughts are no longer his own but those of his filing cabinet. In turn, the machine that gathers and reproduces excerpts is, and remains, a ‘black box’. It is not simply another Ego for enacting a user’s soliloquy but a true Alter Ego with whom the user communicates. Additionally, when the machine is started, the user does not simply refresh his memory; the filing cabinet actually speaks. To achieve this practical outcome, the card index must be provided with a ‘life of its own’ (Eigenleben) which should be as independent of the life of its educator as possible.30 In this sense, the card index functions as a ‘secondary memory’ in Stübel’s terms. This result raises some questions which justify the present article. Is there a socio-structural reason why such an improbability became possible? Is there a trend, in early and late modern society, toward an externalization and technologizing of social memory? And what insight can we gain into intellectual history?
I'm not completely sure I can agree with this. Perhaps I'm missing part of his point?
There is a quirky relationship here to the idea of a personbyte, the complete amount of information and knowledge a person can have. Even misty memories that a person can remember or be reminded of are part of this knowledge. Perfect recall isn't necessary as some things can potentially be reconstituted with some thought towards recreation of an idea.
Compare this with the idea of epic poetry and song of the Yugoslavian guslars. Some may be more artful than others, but at what point are they telling a new story?
Drążkowski, D., Trepanowski, R., & Fointiat, V. (2021). Vaccinating to protect others: The role of self-persuasion and empathy among young adults. PsyArXiv. https://doi.org/10.31234/osf.io/wh4cs
L’enquête a montré le rôle essentiel du directeur d’école en matière d’information des parents d’élèves. Alors que l’utilisation en circonscription de l’application nationale ARIA établit un lien en temps réel entre les écoles et la direction des services départementaux de l’éducation nationale dans le signalement et le suivi des absences des enseignants, le défaut d’outil de communication en direction des parents d’élèves prive ceux-ci d’une information essentielle. C’est souvent à la porte de l’école que les familles apprennent l’absence de l’enseignant.
Johnston, M. (2021). What Lies Beneath: Tackling Vaccine Hesitancy. Emergency Medicine News, 43(10), 7. https://doi.org/10.1097/01.EEM.0000795760.41732.33
Mahase, E. (2021). Covid-19: Vaccine uptake during pregnancy has increased but deprived areas lag behind, data show. BMJ, 375, n2932. https://doi.org/10.1136/bmj.n2932
it builds on the following key pillars: open scientific knowledge, open science infrastructures, science communication, open engagement of societal actors and open dialogue with other knowledge systems.
penerbitan makalah di jurnal open access jelas hanyasebagian kecil saja dari lima pilar kunci: open scientific knowledge, open science infrastructures, science communication, open engagement of societal actors.
Axios treats email as the primary product
It's interesting to think that we've gone through maybe a decade of startups (e.g. Slack) telling us that we need to get away from the chaos of email, and now we're being pitched the idea that email is a quiet, more intimate space.
Newsletters are a great retention tool and a superb distribution tool, with almost no algorithms standing in the way of the audience.
“scannable emails”
Scannable subject lines in emails: "your subject line should tell readers something specific and valuable. Summarize 2–3 of the biggest items in your update and separate them with a comma or em dash so ideas stand out at a glance."
assess the impact of the use of modern technologies on the quality of the education process
technologies
Information and Communication Technology (ICT)
Information and Communication Technology (ICT)
Guarantee access to internet and availability of computers, laptops, or tablets:access to the internet at a decent speed and to proper ICT tools are basicprerequisites for any online teaching and learning strategy.
ICT Information and Communication Technology
Distant and Remote Communication
Distant and Remote Communication
Pugel, J., Long, E. C., Fernandes, M. A., Cruz, K., Giray, C., Crowley, D. M., & Scott, J. T. (n.d.). Who is listening? Profiles of policymaker engagement with scientific communication. Policy & Internet, n/a(n/a). https://doi.org/10.1002/poi3.273
Otte, J. (2021, November 11). ‘No jab, no job’: Care home workers in England on the Covid vaccine mandate. The Guardian. https://www.theguardian.com/society/2021/nov/11/england-care-home-workers-on-mandatory-covid-vaccines
Zubek, J., Ziembowicz, K., Pokropski, M., Gwiaździński, P., Denkiewicz, M., & Boros, A. (2021). Rhythms of the day: How electronic media and daily routines influence mood during COVID-19 pandemic. PsyArXiv. https://doi.org/10.31234/osf.io/czg27
Chen, W., & Zou, Y. (2021). Why Zoom Is Not Doomed Yet: Privacy and Security Crisis Response in the COVID-19 Pandemic. SocArXiv. https://doi.org/10.31235/osf.io/mf935
ReconfigBehSci. (2021, November 2). The current JCVI minutes debate clearly illustrates the problems with Twitter and scientific debate: Meaning glossed, hedges and distinctions left behind, claims about arguments conflated with claims about people, paving the way to ramped up, emotive soundbites and claims. 1/7 [Tweet]. @SciBeh. https://twitter.com/SciBeh/status/1455458854637117440
ReconfigBehSci. (2021, October 31). Please join us at our upcoming workshop on ‘Science Communication as Collective Intelligence’ featuring talks (@SpiekermannKai, @dgurdasani1), panel discussions (@kakape,@CaulfieldTim, @joshua_a_becker, @suneman, @GeoffreySupran and more!) 1/2 https://t.co/isupbnF6yA [Tweet]. @SciBeh. https://twitter.com/SciBeh/status/1454763345748414465
Indie_SAGE - YouTube. (n.d.). Retrieved 31 October 2021, from https://www.youtube.com/channel/UCqqwC56XTP8F9zeEUCOttPQ
Covering COVID-19 vaccine boosters: 4 tips and a timeline. (n.d.). Retrieved October 25, 2021, from https://journalistsresource.org/home/covid-19-boosters-tip-sheet/
Thaker, J., & Richardson, L. (2021). COVID-19 Vaccine Segments in Australia: An Audience Segmentation Analysis to Improve Vaccine Uptake [Preprint]. PsyArXiv. https://doi.org/10.31234/osf.io/y85nm
A recent survey found that only 14% of people they surveyed in the United States talk about climate change. A previous Yale study found that 35% either discuss it occasionally or hear somebody else talk about it. Those are low for something that over 70% of people are worried about.
Conversation is not happening! There is a leverage point in holding open conversations where we understand each other’s language of different cultural groups. Finding common ground, the common human denominators (CHD) between polarized groups is the lynchpin.
For a talk at one conservative Christian college, Dr. Hayhoe – an atmospheric scientist, professor of political science at Texas Tech University, and the chief scientist for The Nature Conservancy – decided to emphasize how caring about climate change is in line with Christian values and, ultimately, is “pro-life” in the fullest sense of that word. Afterward, she says, people “were able to listen, acknowledge it, and think about approaching [climate change] a little differently.”
We often talk about the same things, share the same values, have the same common human denominators, but couched in different language. It is critical to get to the root of what we have in common in order to establish meaningful dialogue.
I was speaking in Iowa, and I was asked, “How do you talk to people in Iowa about polar bears?” I said, “You don’t; you talk to them about corn.” If we begin a conversation with someone with something we already agree on, then the subtext is: “You care about this, and I care too. We have this in common.”
This stresses the importance of applying Deep Humanity wisely by finding the most compelling, salient and meaningful common human denominators appropriate for each conversational context. Which group are we interacting with? What are the major landmarks embedded in THEIR salience landscape?
The BEing journeys we craft will only be meaningful and impactful if they are appropriately matched to the cultural context.
The whole mind- body understanding of how we cognitively construct our reality, via Deep Humanity BEing journeys, can help shift our priorities.
I am frequently shamed for not doing enough. Some of that comes from the right side of the [political] spectrum, but increasingly a larger share of that shaming comes from people at the opposite end of the spectrum, who are so worried and anxious about climate impacts that their response is to find anyone who isn’t doing precisely what they think they should be doing and shame them.
Love, or recognizing the other person in the other tribe as sacred, is going to connect with that person because we are, after all, all of us are human INTERbeings, and love is the affective variable that connects us while shame is a variable that DISconnects us. Love is , in fact, one of our most powerful common human denominators.
UGC (user-generated content) en partageant les photos esthétiques prises par votre communauté. Opter pour une stratégie de marketing d’influence peut aussi s’avérer être une option intelligente.
UGC cine cite
Découvrez les conseils de Digitalis pour créer du contenu ✨ aesthetic ✨ engageant : Respectez les codes du courant esthétique choisi (symboles phares, musique, couleurs, filtre, références culturelles…).Misez tout sur la photographie ou le visuel (un tableau peut parfois suffire).Soignez votre branding général.Mettez-y de l’humain (tendance de l’incarnation).Pensez à établir une stratégie de hashtags pertinents.
Les 5 recommandations
Si un courant est en phase avec votre stratégie social media, rejoint votre univers et que vous en comprenez parfaitement les codes alors vous avez tout intérêt à y aller. Surtout si vous êtes un musée.
conseil strat
How online misinformation spreads. (n.d.). Retrieved October 19, 2021, from https://knowablemagazine.org/article/society/2021/how-online-misinformation-spreads
b) Modalités de diffusionLes documents remis par les associations sont distribués aux élèves pour être donnés à leurs parents au fur et à mesure de leur remise.
Dans le cadre des mesures que le conseil d’école ou le conseil d’administration adopte sur la conduite du dialogue avec les parents ou dans le cadre du projet d’école ou du projet d’établissement, il appartient à chaque école et à chaque établissement de définir, compte tenu de ses spécificités (type d’établissement, population scolaire, nombre d’élèves....), les mesures les mieux à même de porter ces résultats à la connaissance des parents
Les modalités de diffusion des documents sont définies en concertation entre le directeur d’école ou le chef d’établissement et les associations de parents d’élèves.
Ainsi, lors de sa première réunion, le conseil d’école ou le conseil d’administration examine les conditions d’organisation du dialogue avec les parents. Celui-ci doit en effet être renforcé, ce qui suppose de définir précisément les modalités d’information des parents d’élèves, les conditions d’organisation des rencontres avec les parents et de garantir aux associations de parents d’élèves et aux représentants des parents les moyens d’exercer pleinement leurs missions.
Les modalités de diffusion des documents sont définies en concertation entre le directeur d’école ou le chef d’établissement et les associations de parents d’élèves
III.3 La possibilité de rendre compte de l’exercice du mandat Tout représentant des parents d’élèves, qu’il soit ou non membre d’une association, doit pouvoir rendre compte des travaux des instances dans lesquelles il siège
Feehan, J., Husaric, M., & Apostolopoulos, V. (n.d.). No, COVID vaccines don’t stay in your body for years. The Conversation. Retrieved 11 October 2021, from http://theconversation.com/no-covid-vaccines-dont-stay-in-your-body-for-years-169247
Rohlinger, D. A., & Meyer, D. S. (2021). Protest During a Pandemic: How COVID-19 Affected Social Movements in the U.S. SocArXiv. https://doi.org/10.31235/osf.io/qk25r
ReconfigBehSci on Twitter: ‘RT @STWorg: Updates to the wiki of COVID-19 vaccine misinformation: Safety syringes retract: Https://t.co/q7Y1kV7pio Fertility not affe…’ / Twitter. (n.d.). Retrieved 10 October 2021, from https://twitter.com/SciBeh/status/1398370401319673858
EuroPCom. (n.d.). Retrieved October 10, 2021, from https://cor.europa.eu/en/events/Pages/europcom.aspx
Before the use of computers, scientific knowledge was mainly recorded on paper, using three forms of notation: written language, images, and tables. Written text combines plain language, domain-specific vocabulary, and shorthand notation such as mathematical formulas. Images include both drawings and observations captured in photographs, radiographs, etc. Tables represent datasets, which are most often numerical.
On the relationship between media, representation, communication and thinking, this part remembers me of Bret's Victor Media for Thinking the Unthinkable
In some talk, I don't remember if this one, Victor says that using printing media as the main medium for communication is kind of an historical accident. It could be sound, or other media as main representation/communication vehicle.
On my own memories, I remember thinking the relationship between representation and processing/cognition in my early undergrad years as a freshmen, when I saw the two notations for derivates (Leibnitz's and Newton's) and how both make some kind of operations easier (or not). The example I came with, to explain such insight to my postgrad education sciences students later, without appealing to calculus was multiplying in roman numbers versus in arabic ones (and example I would find years later is also employed by Victor)
Sutton, J. (2018). Health Communication Trolls and Bots Versus Public Health Agencies’ Trusted Voices. American Journal of Public Health, 108(10), 1281–1282. https://doi.org/10.2105/AJPH.2018.304661
Palm, R., Bolsen, T., & Kingsland, J. T. (2021). The Effect of Frames on COVID-19 Vaccine Resistance. Frontiers in Political Science, 3, 661257. https://doi.org/10.3389/fpos.2021.661257
Covid: Royal Bolton Hospital taking “urgent action” over virus. (2021, May 25). BBC News. https://www.bbc.com/news/uk-england-manchester-57242368
The Conspiracy Theory Handbook | Center For Climate Change Communication. (n.d.). Retrieved March 3, 2021, from https://www.climatechangecommunication.org/conspiracy-theory-handbook/
Quantifying The COVID-19 Public Health Media Narrative Through TV & Radio News Analysis – The GDELT Project. (n.d.). Retrieved May 14, 2021, from https://blog.gdeltproject.org/quantifying-the-covid-19-public-health-media-narrative-through-tv-radio-news-analysis/
NATO StratCom COE. (2021, January 27). #StratComTalks Vaccines and Disinformation. https://www.youtube.com/watch?v=KcHWs0YeXqA
It is not only the essence of being human but also a vital property of life. Technological advances in communication shape society and lnake its members more interdependent
Lorenz-Spreen, P., Lewandowsky, S., Sunstein, C. R., & Hertwig, R. (2020). How behavioural sciences can promote truth, autonomy and democratic discourse online. Nature Human Behaviour, 4(11), 1102–1109. https://doi.org/10.1038/s41562-020-0889-7
Vraga, E. K., & Bode, L. (2017). Using Expert Sources to Correct Health Misinformation in Social Media. Science Communication, 39(5), 621–645. https://doi.org/10.1177/1075547017731776
Lazić, A., & Zezelj, I. (2021). Negativity In Online News Coverage Of Vaccination Rates In Serbia: A Content Analysis. PsyArXiv. https://doi.org/10.31234/osf.io/nqjb9
https://threadreaderapp.com/thread/1442414902761689088.html Problematic is "problematic". This meta discussion does what it advises.
Moran, M. B., Lucas, M., Everhart, K., Morgan, A., & Prickett, E. (2016). What makes anti-vaccine websites persuasive? A content analysis of techniques used by anti-vaccine websites to engender anti-vaccine sentiment. Journal of Communication in Healthcare, 9(3), 151–163. https://doi.org/10.1080/17538068.2016.1235531
Mixing science and art to make the truth more interesting than lies. (n.d.). Retrieved September 28, 2021, from https://theconversation.com/mixing-science-and-art-to-make-the-truth-more-interesting-than-lies-100221?utm_source=twitter&utm_medium=bylinetwitterbutton
Jamison, A. M., Broniatowski, D. A., Dredze, M., Sangraula, A., Smith, M. C., & Quinn, S. C. (2020). Not just conspiracy theories: Vaccine opponents and proponents add to the COVID-19 ‘infodemic’ on Twitter. Harvard Kennedy School Misinformation Review, 1(3). https://doi.org/10.37016/mr-2020-38
Il importe de leur donner une information la plus complète et la plus claire possible quant à l’organisation des élections des représentants de parents d’élèves
Things start to get a bit more challenging for new entrants to the field. It’s true that this language can initially be a blocker. In fact it can be super frustrating when talking to an expert and they say a bunch of things you don’t understand. I’ve been in plenty of situations in my career where somebody has said something in a casual, confident tone and I’ve feigned understanding, only to go and look up the term later.
In writing there are usually style rules when an acronym or technical term is expanded or defined in its first use for readers. We should make a habit of deliberately doing this, as well as using links to a shared definition in a wiki etc). In speech, this should also be done.
Treatment can depend on how severe a person’s symptoms are.
That's correct because you can't treat all the cases with same treatment.
Pneumonia can be mild, severe, or anything in between. Milder symptoms can include a cough, chills, fever, and shortness of breath.
I agree because most of the patients that come to the hospital have the same signs and symptoms and even worse in some cases.
I was able to secure my current full time job because I was the best communicator and had one of the best interviews. I know my coding skills were no where near other candidates but I was told that they couldn’t communicate well.
Chan, H. F., Rizio, S. M., Skali, A., & Torgler, B. (2021). Early COVID-19 Government Communication Is Associated With Reduced Interest in the QAnon Conspiracy Theory. Frontiers in Psychology, 12, 3503. https://doi.org/10.3389/fpsyg.2021.681975
What I propose, therefore, is to look at motivation as it relates to the c.n.s. -- or conceptual nervous system -- of three different periods: as it was before l930, as it was say 10 years ago, and as it is today. I hope to persuade you that some of our current troubles with motivation are due to the c.n.s. of an earlier day, and ask that you look with an open mind at the implications of the current one. Today's physiology suggests new psychological ideas, and I would like to persuade you that they make psychological sense, no matter how they originated. They might even provide common ground -- not necessarily agreement, but communication, something nearer to agreement -- for people whose views at present may seem completely opposed. While writing this paper I found myself having to make a change in my own theoretical position, as you will see, and though you may not adopt the same position you may be willing to take another look at the evidence, and consider its theoretical import anew. Before going on it is just as well to be explicit about the use of the terms motivation and drive. "Motivation" refers here in a rather general sense to the energizing of behavior, and especially to the sources of energy in a particular set of responses that keep them temporarily dominant over others and account for continuity and direction in behavior. "Drive" is regarded as a more specific conception about the way in which this occurs: a hypothesis of motivation, which makes the energy a function of a special process distinct from those S-R or cognitive functions that are energized. In some contexts, therefore, "motivation" and "drive" are interchangeable.
Looking at past views, the 1930s, a time as the article says that is 10 years in the past and the present. It is important to look at this throughout the years to know where it started, how its evolved and where it could possibly evolve.
We also need to be able to keep an open mind and be able to communicate with those who either totally disagree or are not quite on board with our own views.
The author is breaking down motivation as it relates to the c.n.s during these time periods.
Maftei, A., & Holman, A. C. (2021). SARS-CoV-2 Threat Perception and Willingness to Vaccinate: The Mediating Role of Conspiracy Beliefs. Frontiers in Psychology, 12, 672634. https://doi.org/10.3389/fpsyg.2021.672634
Thorpe, A., Fagerlin, A., Butler, J., Stevens, V., Drews, F. A., Shoemaker, H., Riddoch, M., & Scherer, L. D. (2021). Communicating about COVID-19 vaccine development and safety [Preprint]. Public and Global Health. https://doi.org/10.1101/2021.06.25.21259519
While it is clear that technologies of communication change societiesand permit different forms of human organization, it is not clear that theychange the basic human thought processes embedded in language. The humanbrain does adapt differently to different technologies (recall the differences inbrain wiring between readers of ideograms and of phonetic alphabets), butthe evidence to date indicates the human brain adapts in order to translateinformation into language, so as to exchange information and permit concertedaction with others with whom we communicate. This concerted action is nolonger, as at the dawn of language, action undertaken by people in close contactbut rather is activity undertaken because of reliance upon expectations storedin individual and social memory.
Blais, J., Babchishin, K. M., & Hanson, R. K. (2021). Improving our Risk Communication: Standardized Risk Levels for BARR-2002R. PsyArXiv. https://doi.org/10.31234/osf.io/2xr3m
Vandeweerdt, C., Luong, T., Atchapero, M., Mottelson, A., Holz, C., Makransky, G., & Böhm, R. (2021). Virtual reality reduces COVID-19 vaccine hesitancy in the wild. PsyArXiv. https://doi.org/10.31234/osf.io/sq9yc
Zarzeczna, N., Hanel, P. H. P., Rutjens, B., Bono, S. A., Chen, Y.-H., & Haddock, G. (2021). Scientists, speak up! Source impacts trust in and intentions to comply with health advice cross-culturally. PsyArXiv. https://doi.org/10.31234/osf.io/279yg
ReconfigBehSci on Twitter: “@ToddHorowitz3 ok, but I would have hoped that in an ideal public communication medium for science, people had megaphones that were commensurate with their skills and expertise, if there was variation among platform members at all. And I’d hope that users were calibrated re own expertise” / Twitter. (n.d.). Retrieved August 10, 2021, from https://twitter.com/SciBeh/status/1423710934925598725
Gretton, J. D., Meyers, E. A., Walker, A. C., Fugelsang, J. A., & Koehler, D. (2021). A Brief Forewarning Intervention Overcomes Negative Effects of Salient Changes in COVID-19 Guidance. PsyArXiv. https://doi.org/10.31234/osf.io/gbqw3
Dai, H., Saccardo, S., Han, M. A., Roh, L., Raja, N., Vangala, S., Modi, H., Pandya, S., Sloyan, M., & Croymans, D. M. (2021). Behavioral Nudges Increase COVID-19 Vaccinations. Nature. https://doi.org/10.1038/s41586-021-03843-2
Pillai, Raunak, and Lisa Fazio. “The Effects of Repeating False and Misleading Information on Belief.” PsyArXiv, August 3, 2021. https://doi.org/10.31234/osf.io/z78xm.
Escandón, K., Rasmussen, A. L., Bogoch, I. I., Murray, E. J., Escandón, K., Popescu, S. V., & Kindrachuk, J. (2021). COVID-19 false dichotomies and a comprehensive review of the evidence regarding public health, COVID-19 symptomatology, SARS-CoV-2 transmission, mask wearing, and reinfection. BMC Infectious Diseases, 21(1), 710. https://doi.org/10.1186/s12879-021-06357-4